Скалярное произведение в координатах.
Покажем как скалярное произведение вычисляется через координаты векторов в прямоугольной системе координат на плоскости и в пространстве.
Определение.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов 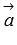 и
и 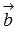 .
.
То есть, для векторов  на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид
на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид
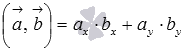 ,
,
а для векторов  в трехмерном пространстве скалярное произведение в координатах находится как
в трехмерном пространстве скалярное произведение в координатах находится как
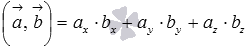 .
.
Таким образом, мы имеем третье определение скалярного произведения. Покажем, что это определение эквивалентно первому.
Сначала докажем равенства  для векторов
для векторов  на плоскости, заданных в прямоугольной декартовой системе координат.
на плоскости, заданных в прямоугольной декартовой системе координат.
Отложим от начала координат (точка О) векторы  и
и  . Тогда
. Тогда  (при необходимости обращайтесь к статьямоперации над векторами и их свойства и операции над векторами в координатах).
(при необходимости обращайтесь к статьямоперации над векторами и их свойства и операции над векторами в координатах).
Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов мы можем записать  . Так как
. Так как  , то последнее равенство можно переписать как
, то последнее равенство можно переписать как 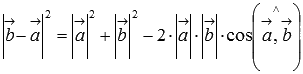 , а по первому определению скалярного произведения имеем
, а по первому определению скалярного произведения имеем 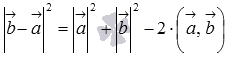 , откуда
, откуда 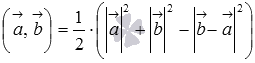 .
.
Вспомнив формулу вычисления длины вектора по координатам, получаем

Абсолютно аналогично доказывается справедливость равенств  для векторов
для векторов  , заданных в прямоугольной системе координат трехмерного пространства.
, заданных в прямоугольной системе координат трехмерного пространства.
Формула скалярного произведения векторов в координатах позволяет заключить, что скалярный квадрат вектора равен сумме квадратов всех его координат: на плоскости  , в пространстве
, в пространстве  .
.