СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ. СВОЙСТВА ВЫСЧИСЛЕНИЯ

Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.

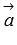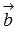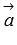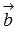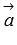Скалярное произведение векторов и будем обозначать как . Тогда формула для вычисления скалярного произведения имеет вид , где и - длины векторов и соответственно, а - угол между векторами и .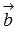

Из определения скалярного произведения видно, что если хотя бы один из умножаемых векторов нулевой, то .

Вектор можно скалярно умножить на себя. Скалярное произведение вектора на себя равно квадрату его длины, так как по определению .

Определение.

Скалярное произведение вектора на себя называется скалярным квадратом.

Формулу для вычисления скалярного произведения можно записать в виде , где - числовая проекция вектора 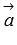на направление вектор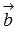а , а - числовая проекция вектора 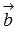на направление вектора .

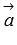Таким образом, можно дать еще одно определение скалярного произведения двух векторов.

Определение.

Скалярным произведением двух векторов 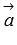и 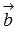называется произведение длины вектора 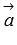на числовую проекцию вектора 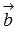на направление вектора 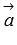или произведение длины вектора 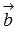на числовую проекцию вектора 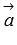на направление вектора .

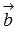Это определение эквивалентно первому.