T-распределение Стьюдента

t-распределение Стьюдента - это непрерывное одномерное распределение с одним параметром - количеством степеней свободы. Форма распределения Стьюдента похожа на форму нормального распределения (чем больше число степеней свободы, тем ближе распределение к нормальному). Отличием является то, что хвосты распределения Стьюдента медленнее стремятся к нулю, чем хвосты нормального распределения.

Обычно распределение Стьюдента появляется в задачах, связанных с оценкой математического ожидания нормально распределенных случайных величин. Пусть X₁ , ..., X_n - независимые случайные величины, нормально распределенные с математическим ожиданием μ и дисперсией σ ². Тогда мы можем получить следующие оценки для параметров μ и σ ²:

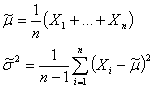
При этом оценка математического ожидания не равна в точности μ, а лишь колеблется вокруг этой величины. Разность истинного математического ожидания и рассчитанного на основе выборки, поделенная на масштабирующий коэффициент

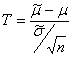
имеет распределение, которое называется распределением Стьюдента с N степенями свободы. Есть и другие разделы статистики, в которых появляются случайные величины, распределенные по Стьюденту. Например, распределение Стьюдента используется при оценке значимости коэффициента корреляции Пирсона.

 

Чаще всего критерий Стьюдента применяется для проверки равенства средних значений в двух выборках.

Пример 1. Первая выборка — это пациенты, которых лечили препаратом А. Вторая выборка — пациенты, которых лечили препаратом Б. Значения в выборках — это некоторая характеристика эффективности лечения (уровень метаболита в крови, температура через три дня после начала лечения, срок выздоровления, число койко-дней, и т.д.) Требуется выяснить, имеется ли значимое различие эффективности препаратов А и Б, или различия являются чисто случайными и объясняются «естественной» дисперсией выбранной характеристики.

Пример 2. Первая выборка — это значения некоторой характеристики состояния пациентов, записанные до лечения. Вторая выборка — это значения той же характеристики состояния тех же пациентов, записанные после лечения. Объёмы обеих выборок обязаны совпадать; более того, порядок элементов (в данном случае пациентов) в выборках также обязан совпадать. Такие выборки называются связными. Требуется выяснить, имеется ли значимое отличие в состоянии пациентов до и после лечения, или различия чисто случайны.

 

12 Основные распределения, используемые в математической статистике:

F-распределение Фишера. Примеры использования распределения.

 

Если у нас есть две случайные величины, Y₁ и Y₂ , имеющие распределение хи-квадрат со степенями свободы a и b соответственно, то их отношение

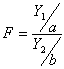
имеет распределение, которое называется F-распределением со степенями свободы a и b. Также это распределение известно, как распределение Фишера.

Функция плотности вероятности F-распределения для некоторых a и b приведена на графике справа. Её аналитическая форма имеет вид:

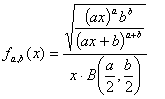
Интегральная функция вероятности F-распределения имеет вид:

 

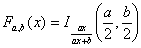
С помощью нормального распределения определяются три распределения, которые в настоящее время часто используются при статистической обработке данных. В дальнейших разделах книги много раз встречаются эти распределения.

Распределение Пирсона 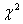(хи - квадрат) – распределение случайной величины

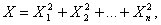
где случайные величины X₁, X₂,…, X_n независимы и имеют одно и тоже распределение N(0,1). При этом число слагаемых, т.е. n, называется «числом степеней свободы» распределения хи – квадрат.

Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных [8, 9, 11, 16].

Распределение t Стьюдента – это распределение случайной величины

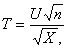
где случайные величины U и X независимы, U имеет распределение стандартное нормальное распределение N(0,1), а X – распределение хи – квадрат с n степенями свободы. При этом n называется «числом степеней свободы» распределения Стьюдента.

Распределение Стьюдента было введено в 1908 г. английским статистиком В. Госсетом, работавшем на фабрике, выпускающей пиво. Вероятностно-статистические методы использовались для принятия экономических и технических решений на этой фабрике, поэтому ее руководство запрещало В. Госсету публиковать научные статьи под своим именем. Таким способом охранялась коммерческая тайна, «ноу-хау» в виде вероятностно-статистических методов, разработанных В. Госсетом. Однако он имел возможность публиковаться под псевдонимом «Стьюдент». История Госсета - Стьюдента показывает, что еще сто лет назад менеджерам Великобритании была очевидна большая экономическая эффективность вероятностно-статистических методов.

В настоящее время распределение Стьюдента – одно из наиболее известных распределений среди используемых при анализе реальных данных. Его применяют при оценивании математического ожидания, прогнозного значения и других характеристик с помощью доверительных интервалов, по проверке гипотез о значениях математических ожиданий, коэффициентов регрессионной зависимости, гипотез однородности выборок и т.д. [8, 9, 11, 16].

Распределение Фишера – это распределение случайной величины

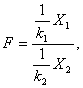
где случайные величины Х₁ и Х₂ независимы и имеют распределения хи – квадрат с числом степеней свободы k₁ и k₂ соответственно. При этом пара (k₁, k₂) – пара «чисел степеней свободы» распределения Фишера, а именно, k₁ – число степеней свободы числителя, а k₂ – число степеней свободы знаменателя. Распределение случайной величины F названо в честь великого английского статистика Р.Фишера (1890-1962), активно использовавшего его в своих работах.

Распределение Фишера используют при проверке гипотез об адекватности модели в регрессионном анализе, о равенстве дисперсий и в других задачах прикладной статистики [8, 9, 11, 16].

Выражения для функций распределения хи - квадрат, Стьюдента и Фишера, их плотностей и характеристик, а также таблицы, необходимые для их практического использования, можно найти в специальной литературе (см., например, [8]).

 

13 Геометрическое распределение, параметры распределения

 

Со схемой испытаний Бернулли можно связать еще одну случайную величину x - число испытаний до первого успеха. Эта величина принимает бесконечное множество значений от 0 до + 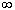и ее распределение определяется формулой

p_k = P(x= k) = q^k-1 p, 0 <p <1, k=1, 2, … , , , .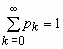

 

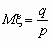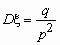Пусть проводятся независимые испытания, каждое испытание может иметь два исхода: удача с вероятностью p и неудача с вероятностью q = 1 - p. Введем в рассмотрение случайную величину X — число испытаний до первого появления удачи. Эта случайная величина может принимать значения 1, 2, 3, 4 и так далее до бесконечности. Когда говорят, что случайная величина X имеет значение k, то это означает, что первые k - 1 испытание закончились неудачей, а k-ое испытание стало удачным. Вероятность того, что в серии независимых испытаний будет вначале k - 1 неудач, а в k-ое испытание — удача, равна 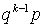. Таким образом мы получили закон распределения случайной величины X: значению k случайной величины соответствует вероятность 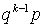. Этот закон распределения и называется геометрическим распределением . 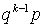Название происходит из того, что величина представляет собой геометрическую прогрессию, с первым членом p и знаменателем q.Изучим теперь свойства этого распределения. С ростом k вероятности убывают. Используя формулу для суммы членов геометрической прогрессии, можем записать: 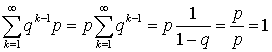, то есть условие, что сумма всех вероятностей в законе распределения равна единице, выполнено. Вычислим теперь математическое ожидание и дисперсию. По определению математического ожидания имеем: 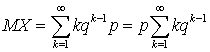. Для вычисления суммы воспользуемся следующим приемом — заменим 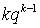на 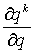и вынесем производную за знак суммы, в итоге получим: 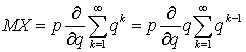. Оставшаяся сумма представляет собой сумму членов геометрической прогрессии и равна . Вычисляя производную, запишем: . Аналогично можно получить выражение для : . Заменяя сумму на ее значение , вычисляем: . Таким образом, имеем выражение для дисперсии: . Если вероятность удачи равна единице, то математическое ожидание числа испытаний до первой удачи равно 1, а дисперсия — 0. Если, наоборот, вероятность удачи равна нулю, то математическое ожидание — бесконечность (то есть нужно произвести бесконечное число испытаний до появления удачи).