Выборочные оценки числовых характеристик.

Оценка числовых характеристик и параметров распределения
(Несгруппированные результаты)

После отбрасывания всех сомнительных результатов ряд содержит n измерений x_i (где i = 1, 2, 3, …, n), некоторые из которых могут иметь одинаковое значение.

Математическое ожидание представляемого этим рядом нормального распределения оценивается средним арифметическим 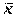для результатов:

, (4)

Оценка стандартного отклонения
(Несгруппированные результаты)

Стандартное отклонение по квадратам отклонений результатов измерений от среднего арифметического определяется по формуле:

, (7)

где x- значение i -го измерения (i = 1, 2, 3, …, n);

n- общее число измерений;

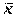- среднее арифметическое n измерений, вычисленное в соответствии с п. 6.1.1.

Чтобы облегчить вычисление, рекомендуется следующая формула:

. (8)
Вычисление выборочных характеристик при малом объеме выборки

6.3.1 Выборочное среднее 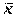определяется в соответствии с п. 6.1.1.

6.3.2 Выборочная медиана при нечетном объеме выборки n = 2m – 1 равна среднему члену вариационного рада Х _0,5 = Х_m. При четном объеме n = 2m медиана равна среднему значению двух средних значений вариационного ряда:

. (11)

6.3.3 Выборочная дисперсия

D = S² = 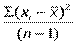, (12)

или

D = [Σ x²_i - (Σx_i) ² ] . (13)

Вычисление выборочных моментов третьего и четвертого порядков при объеме n<50 нецелесообразно в связи с их большими вероятными отклонениями от генеральных моментов. Для нормально распределенной генеральной совокупности оценки среднего, дисперсии являются эффективными, состоятельными и несмещенными.

Несмещенная оценка СКО:

S=k*s,

где k – поправочный коэффициент, зависящий от объема выборки (Приложение Б).