Задание 1. Простые цепи
Математическое моделирование.
Этот этап работы проводится самостоятельно, как подготовка к выполнению аналогового моделирования с помощью приборов.
Он заключается в расчётах электрических цепей с заданными в конкретном варианте значениями элементов. В дальнейшем при аналоговом моделировании эти элементы будут заменены компонентами, номиналы которых будут соответствовать выбранным значениям элементов с заданной погрешностью.
Варианты номиналов элементов
| Вар | ||||||||||||
| R1 Ом | ||||||||||||
| C1 мкФ | 0,1 | 0,1 | 0,1 | 0,1 | 0,068 | 0,068 | 0,068 | 0,068 | 0,047 | 0,047 | 0,047 | 0,047 |
| L1 мГн | 1,2 | 1,2 | 1,5 | 1,5 | 1,8 | 1,8 | 2,2 | 2,2 | 2,7 | 2,7 | ||
| RS Ом | ||||||||||||
| Вар | ||||||||||||
| R1 Ом | ||||||||||||
| C1 мкФ | 0,033 | 0,033 | 0,033 | 0,033 | 0,022 | 0,022 | 0,022 | 0,022 | 0,015 | 0,015 | 0,015 | 0,015 |
| L1 мГн | 3,3 | 3,3 | 3,9 | 3,9 | 4,7 | 4,7 | 5,6 | 5,6 | 6,8 | 6,8 | 8,2 | 8,2 |
| RS Ом |
Задание 1. Простые цепи
Для указанных ниже схем, содержащих один реактивный элемент:
1. Рассчитать значение граничной частоты FB при значениях элементов, указанных в выбранном варианте.
2. Рассчитать значение комплекса выходного напряжения 
и тока источника 
при входном гармоническом сигнале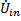 
= 2 B, а также частотах F=FB; 0,5 FB; 1,5 FB.
Построить примерный вид осциллограмм и 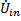и фазовые диаграммы напряжений с указанием тока источника.
3. Рассчитать значение полной, активной и реактивной мощности, выделяющихся в данных электрических схемах при всех трёх частотах. Построить треугольники мощностей.
Пример
1) Для схем, содержащих один активный и один реактивный элементы, на зависимости K(ω)=Uвых/Uвх имеется одна характерная точка, которая называется граничной частотой FB. Она определяется просто – при этой частоте напряжения на элементах равны. То есть при одинаковом токе на этой частоте равны их сопротивления и реактансы. Отсюда ωL=R и 1/ωC=R, или FB=R/2πL и FB=1/2πRC соответственно. В этой точке значение K(FB)=1/√2, а значение разности фаз между входным и выходным напряжением равно ±π/4 (см. лекции). Далее следует подставить значения элементов из Вашего варианта для схем, указанных в соответствующем задании и занести эти данные в таблицы результатов.
2) Ток в одноконтурных электрических цепях с применением комплексов вычисляется очень просто: 
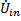= /R+jХL 
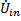= /R-jХC , где XL=ωL, XC=1/ωC – реактансы элементов
Отсюда, в зависимости от того какой элемент будет выходным, в цепи с индуктивностью =R· 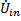/R+jХL или =jXL· 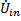/R+jХL а в цепи с конденсатором соответственно
=R· 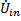/R-jХc или =-jXC· 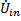/R-jХc
Для перехода от комплексов к реальным значениям токов i(ωt) и напряжений u(ωt) нужно рассчитать модули и разности фаз полученных комплексных чисел по известным формулам. Тогда будет удобно записать полученные реальные значения токов и напряжений в тригонометрической форме Aej(ωt±φ).
Далее следует занести полученные данные в рекомендуемые таблицы, построить фазовую диаграмму, а также развёртки синусоид с рассчитанными разностями фаз (масштаб выбирается самостоятельно).
| Вариант | R Ом | С мкФ | L мГн |
| F, кГц |
|  Aejφ
| Aejφ
| мощность S=P+jQ | ||||||||||
| S | P | Q | ||||||||||||
| расч | эксп | расч | эксп | расч | эксп | расч | эксп | расч | эксп | расч | эксп | расч | эксп | |
| Fb | 2ej0° | |||||||||||||
| 0,5Fb | 2ej0° | |||||||||||||
| 1,5Fb | 2ej0° |
3) Расчёт мощностей рекомендуется начать с полной мощности 
, затем перевести полученное значение в алгебраическую форму. Тогда действительная и мнимая часть полученного значения будут представлять активную и реактивную мощность.
Схема 1-1, дифференцирующая RC-цепь.
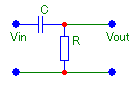
Схема 1-2, интегрирующая RC-цепь.
Схема 1-3, дифференцирующая LR-цепь
Схема 1-4, интегрирующая LR-цепь.
