Основные понятия и определения по теме
Для характеристики изучаемой совокупности по количественным признакам используются различные показатели, в том числе и средние величины, которые показывают средний уровень изучаемого признака.
Средние величины используются в здравоохранении:
– для оценки здоровья населения (показатели физического развития, средняя длительность пребывания на больничном листе и т.д.);
– для оценки деятельности лечебно-профилактических учреждений (средняя длительность работы койки в году, оборот койки и т.д.);
– для планирования (число жителей на терапевтическом, педиатрическом участке, стоимость одного койко-дня и т.д.);
– для оценки санитарно-гигиенических параметров (освещенность, температура, влажность воздуха и т.д.);
– для определения разовых доз лекарственных веществ и т.д.
Средний уровень изучаемого явления – одно из групповых свойств статистической совокупности. Средний уровень измеряют с помощью критериев, которые носят название средних величин.
Средние величины обладают тремя свойствами:
– средняя занимает срединное положение в вариационном ряду;
– средняя выражает общую меру изучаемого явления;
– сумма отклонений всех вариант от средней равна нулю.
Наиболее широко используются три средние величины:
– мода (Мо) – соответствует величине признака, который чаще встречается в статистической совокупности, т.е. варианте наиболее часто встречающейся в вариационном ряду;
– медиана (Ме) – варианта, занимающая срединное положение в вариационном ряду и делящая его пополам. Для того, чтобы узнать значение медианы, необходимо определить порядковый номер варианты, занимающей срединное положение (n/2), где n – число вариант в вариационном ряду. При нечетном числе вариант используется формула n+1/2;
– средняя арифметическая (простая, взвешенная).
Для определения средних величин в статистической совокупности необходима предварительная обработка и систематизация данных исследования, а именно, построение вариационного ряда.
Вариационный ряд – это ряд числовых измерений определенного признака, отличающихся друг от друга по величине и расположенных в определенном порядке.
Вариационный ряд может быть:
– простой, несгруппированный;
– сгруппированный;
– прерывный или непрерывный;
– правильный или неправильный;
– ранжированный или неранжированный.
Обозначения, используемые в вариационном ряду:
– варианта (V) – отдельное числовое выражение изучаемого признака;
– частота (р) – количество вариант определенной величины;
– число наблюдений (n) – общее число вариант в вариационном ряду.
Если число наблюдений не превышает 30, то варианты можно расположить по возрастанию или убыванию, т.е. построить простой вариационный ряд.
Пример: получены данные о длительности лечения в поликлинике 45 больных ангиной (в днях): 20, 18, 19, 16, 17, 16, 14, 13, 15, 14, 15, 13, 12, 13, 3, 4, 12, 11, 12, 11, 10, 12, 11, 10, 11, 8, 7, 11, 11, 10, 10, 10, 9, 8, 8, 9, 4, 5, 6, 9, 5, 9, 6, 7, 7.
Строим вариационный ряд:
Таблица 1
| V | åp=45 | ||||||||||||||||||
| p | |||||||||||||||||||
| d | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | ådp=-23 | ||||||||||
| dp | -8 | -14 | -12 | -10 | -12 | -9 | -8 | -5 |
Определяем средние величины:
Мода (Мо) =11, т.к. данная варианта встречается в вариационном ряду наиболее часто (р=6).
Медиана (Ме) – порядковый номер варианты занимающей срединное положение  , это место в вариационном ряду занимает варианта равная 11.
, это место в вариационном ряду занимает варианта равная 11.
Средняя арифметическая (М) позволяет наиболее полно охарактеризовать средний уровень изучаемого признака. Для вычисления средней арифметической используется два способа:среднеарифметический способ и способ моментов.
Если частота встречаемости каждой варианты в вариационном ряду равна 1, то рассчитывают среднюю арифметическую простую, используя среднеарифметический способ: 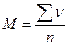 .
.
Если частота встречаемости вариант в вариационном ряду отличается от 1, то рассчитывают среднюю арифметическую взвешенную, по среднеарифметическому способу:  .
.
По способу моментов: А – условная средняя,
 d=V-A, А=Мо=11
d=V-A, А=Мо=11
Если число вариант в вариационном ряду более 30, то строится сгруппированный ряд. Построение сгруппированного ряда:
1) определение Vmin и Vmax Vmin=3, Vmax=20;
2) определение количества групп (по таблице);
3) расчет интервала между группами  ;
;
4) определение начала и конца групп;
5) определение частоты вариант каждой группы (таблица 2).
Таблица 2