Выравнивание показателей динамического ряда
| Годы | Число случаев на 100 раб-х | Укрупнение интервала | Групповая средняя | Скользящая средняя |
| 57,0 | – | |||
| 58,0 | 57+58=115 | (57+58)/2=57,5 | (57+58+64)/3=57,5 | |
| 64,0 | (58+64+48)/3=57,0 | |||
| 48,0 | 64+48=112 | (64+48)/2=56,0 | (64+48+36)/3=49,0 | |
| 36,0 | (48+36+57)/3=47,0 | |||
| 57,0 | 36+57=93 | (36+57)/2=46,5 | (36+57+44)/3=45,7 | |
| 44,0 | (57+44+49)/3=50,0 | |||
| 49,0 | 44+49=93 | (44+49)/2=46,5 | – |
Вывод: Анализируя сам показатель – число случаев на 100 работающих, трудно судить о тенденции его изменения. Проведя выравнивание динамического ряда (любым способом), можно уже говорить о тенденции снижения показателя.
Метод наименьших квадратов
Динамика развития лучше всего может быть выражена линией, которая наиболее близко подходит к фактическим данным. Это достигается методом наименьших квадратов, который наиболее объективно выявляет тенденцию развития изучаемого явления.
Сначала определяется характер изменения изучаемого явления. В зависимости от характера кривой определяют характер уравнения зависимости между явлением и временем.
Имеется много различных уравнений, выражающих зависимость между двумя изучаемыми явлениями. Например, если тенденция прямолинейная, то она представляется в виде прямой линии, уравнение которой y = a + bx (парабола I порядка). Если тенденция криволинейная, то она может быть представлена в виде параболы II порядка (уравнение y = a + bx +cx2), параболой III порядка (y = a + bx +cx2 + dx3) или параболой n-го порядка.
Чаще всего в практике здравоохранения используется выравнивание по параболе I и II порядка.
Проведем выравнивание показателей младенческой смертности, имеющих прямолинейную тенденцию развития, по способу наименьших квадратов, используя параболу I порядка (табл. 2).
Таблица 2
Выравнивание показателей младенческой смертности
по параболе I порядка
| Годы | Показатель младенческой смертности (Y) | Х1 | Х12 | YХ1 | Y1 |
| -4 | -164 | 40,9 | |||
| -3 | -117 | 38,7 | |||
| -2 | -72 | 36,5 | |||
| -1 | -35 | 34,4 | |||
| 32,2 | |||||
| 30,3 | |||||
| 27,06 | |||||
| 25,7 | |||||
| 23,5 | |||||
| ∑Y = 290 | ∑X12 = 60 | ∑YX1 = -130 |
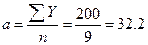

Y1981=32,2+(-2,17)*(-4)=40,9 Y1981=32,2+(-2,17)*(-3)=38,7 и т.д.
Для определения точности выравнивания (аппроксимации) используют формулу: 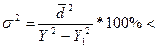 5%
5%
Таблица 3