Основные понятия и определения по теме
Элементы (единицы наблюдения), из которых состоит совокупность, имеют различные по величине значения изучаемого у них признака, и каждое из этих значений встречается в группе с неодинаковой частотой. На достаточно большой совокупности наблюдений можно определить закономерности распределения изучаемого явления (признака).
Значение характера распределения признака в совокупности позволит правильно выбрать статистические критерии для оценки изучаемой совокупности. Распределение признака – с этого начинается оценка статистической совокупности. Как можно оценить распределение признака?
1 – Графически
2 – Статистически.
Графически различают следующие типы распределения:
1) альтернативное;
2) нормальное (симметричное);
3) асимметричное (правостороннее, левостороннее, бимодальное).
Альтернативное распределение имеет только два противоположных значения признака (да или нет). Например, при решении вопроса о госпитализации больного имеется только два решения: госпитализировать, не госпитализировать.
| Да | Нет |
Нормальное (симметричное, гауссовское) распределение обычно наблюдается при изучении количественных признаков (например, рост, масса тела, величина жизненной емкости легких, сроки лечения больных в стационаре и т.д.).
При нормальном типе распределения число случаев наблюдений с различной величиной признака располагаются от меньшего значения к большему, причем наибольшее число случаев наблюдений приходится на середину ряда. Нормальное распределение имеют показатели здоровья больших групп населения. Так как при нормальном распределении можно применить классические, параметрические методы, то, следовательно, они используются при изучении здоровья населения (рис. 1, график а).
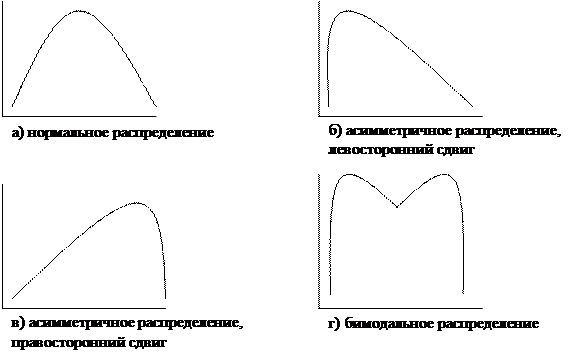 |
Рис. 1. Типы распределения признака в статистической совокупности.
Асимметричное распределение может быть с левосторонним сдвигом (рис. 1, график б, например, кратность прививок в раннем возрасте и у взрослых), с правосторонним сдвигом (график в, например, увеличение хронических заболеваний с возрастом) и бимодальным или двугорбым при неоднородной совокупности (график г, например, при изучении величины среднего роста учеников младших классов, когда в совокупность включается рост мальчиков и девочек).
При асимметричном типе распределения для изучениястатистической совокупности нельзя использовать параметрические методы, а необходимо прибегнуть к непараметрическим методам исследования.
Распределение признака можно изучить и с использованием статистических показателей, которые очень значимы в практике здравоохранения.
В работе врач постоянно сталкивается с различными величинами. В статистике пользуются тремя видами величин:
1–абсолютными,
2–относительными,
3–средними.
Все они дают возможность судить о величине изучаемого явления.
Абсолютные величины – это показатели, выражающие размеры общественных явлений и процессов. По способу выражения этих размеров они подразделяются на индивидуальные и суммарные (итоговые).
Индивидуальные абсолютные величины – это показатели, выражающие размеры количественных признаков у отдельных единиц исследуемых объектов, например, температура тела у конкретного больного, количество больных, принятых врачом за смену.
Суммарные абсолютные показатели дают ответ на поставленный вопрос о сумме единиц наблюдения среды или изучаемого по программе исследования явления. Получаются они в результате непосредственного подсчета единиц наблюдения или суммирования значений количественных признаков, которыми обладают эти единицы. Так, подсчет больниц по данным годовых отчетов дает их численность, а суммирование их коечного фонда – показатель абсолютного его размера (количество больничных коек в крае).
Абсолютные величины служат основой для вычисления относительных и средних величин (например, количество обслуженных вызовов за день, число зарегистрированных заболеваний за год на территории обслуживания поликлиники и др.). Абсолютные величины представлены в учетных (Листок учета врача-стоматолога, Дневник работы врача поликлиники) и отчетных статистических формах.
Хотя абсолютные величины и сами по себе несут важную информацию о размере того или иного явления, но при анализе чаще имеют ограниченное познавательное значение, т.к. по ним трудно судить о частоте, динамике какого-либо явления или дать оценку работы врачей или подразделения (например, в 2012 году в терапевтическом отделении умерло 5 человек, а в 2013 году – 7. Можно ли сказать, что стали умирать чаще? Может быть, через отделение прошло большее число больных?).
Для определения структуры и уровня изучаемого явления, сравнения его в динамике или у различных групп населения, или по отдельным административным территориям пользуются относительными величинами.
Относительные величины (коэффициенты) – выражают количественные соотношения, присущие общественным явлениям и процессам. Получаются они как результат сравнения (отношения, деления) двух абсолютных величин. С относительными величинами мы сталкиваемся в основном при анализе состояния здоровья населения и при анализе деятельности учреждений здравоохранения по данным годового отчета.
Средние величины – характеризуют средний уровень изучаемого признака.
Средние величины используются:
1) при оценке состояния здоровья (показатели физического развития, средняя длительность пребывания больного в стационаре и т.д.);
2) при оценке деятельности лечебно-профилактических учреждений (оборот койки, средняя нагрузка на 1 час работы врача в поликлинике);
3) при оценке лабораторных данных и клинических параметров (нормы параметров гомеостаза, АД, ЖЕЛ);
4) при определении диетических столов для больных (содержание белка, жира, углеводов и т.д.);
5) при оценке санитарно-гигиенических нормативов (температура, загазованность и др.);
6) при определении разовых доз лекарства;
7) при разработке норм и нормативов для планирования.
Относительные величиныв статистике представлены статистическими показателями:
1) экстенсивными;
2) интенсивными;
3) показателями соотношения;
4) показателями наглядности;
5) показателями динамического ряда (см. тему «Динамические ряды и их анализ»).
Экстенсивный показатель – или показатель структуры распределения, удельного веса. Указывает на отношение части к целому или на долю части в целом, т.е. он показывает, какую часть от общего числа всех заболеваний (причин смерти) составляет то или иное заболевание (причина смерти), входящее в общее число. Фактически отвечает на вопрос: какая часть? какая доля? Типичная ошибка, когда по экстенсивному показателю судят о частоте явления и пытаются оценить динамику. Экстенсивным показателем пользуются только для характеристики состава явления в данном месте и в данное время. Выражается этот показатель в процентах.
Вычисляется он по формуле:
Часть явления (или часть среды)
–––––––––––––––––––––––––––––––– х 100%
Явление в целом (или среда в целом)
Например: определить структуру ошибочных диагнозов и провести анализ, если при патологоанатомическом вскрытии умерших оказалось, что в 126 случаях имеется расхождение клинического и патологоанатомического диагноза. В том числе при инфаркте миокарда в 64 случаях, при язвенной болезни желудка и 12-перстной кишки – в 22 и раке легкого в 40 случаях.
Доля расхождения диагнозов при инфаркте миокарда:
126 сл. – 100% 64 сл. – х 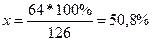
Доля расхождения диагнозов при язвенной болезни:
126 сл. – 100% 22 сл. – х 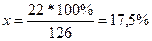
Доля расхождения диагнозов при раке легкого:
126 сл. – 100% 40 сл. – х 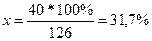
Вывод: из расчета видно, что наибольшая доля ошибочных диагнозов, каждый второй, приходится на инфаркт миокарда. На втором месте – рак легкого. Следовательно, необходимо обратить внимание на повышение квалификации врачей по диагностике этих нозологических форм. В отделении это может быть проведено в виде клинических конференций, семинаров, клинико-патолого-анатомических конференций.
Если нас интересует частота или распространенность какого-либо явления, то вычисляется интенсивный показатель (показатель частоты). Он отвечает на вопрос: как часто болеют, умирают, рождаются и т.д. Для того, чтобы его рассчитать, необходимо знать численность населения или контингента, т.е. среды, продуцирующей это явление.
Вычисляется интенсивный показатель по формуле:
Абс. размер явления
–––––––––––––––––– х 1000 (100, 10 000, 100 000)
Абс. размер среды
При расчете этого показателя следует помнить о следующих требованиях:
1) желательно, чтобы показатель получился целым числом (это облегчает логическое осмысление показателя), отсюда и величина цифры, на которую умножают, т.е. стандарта – 100, 1000, 10 000 и 100 000;
2) сопоставлять можно только те показатели, которые рассчитаны на один и тот же стандарт. Вместе с тем, общепринято, что на 100 вычисляются показатели летальности, заболеваемости с временной утратой трудоспособности, патологической пораженности; на 1000 – показатели общей заболеваемости, выявляемости, некоторые демографические показатели; на 10 000 – показатели соотношения (обеспеченности); на 100 000 – показатель смертности по отдельным причинам. Чем реже встречается явление, тем большее число берется в качестве стандарта.
Например: население Н-ского района 21 000 человек. В 2012 г. зарегистрировано 18 756 впервые выявленных случаев заболеваний. Вычислить показатель первичной заболеваемости (incidence):
на 21 000 – 18 756 сл.
на 1 000 – х 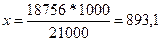 ‰.
‰.
Вывод: в 2012 году в Н-ском районе на каждую 1000 населения было зарегистрировано 893,1 случаев вновь выявленных заболеваний. В данном случае необходимо для составления реального плана работы выяснить:
1) какая нозологическая форма поддерживает высокий уровень первичной (собственно, истинно, incidence) заболеваемости;
2) среди какого контингента в основном поддерживается такой высокий уровень заболеваемости;
3) причины этого явления;
4) не было ли вспышки сезонных заболеваний?
Показатель соотношения (обеспеченности) – это разновидность интенсивного показателя, но он характеризует отношение между разнородными величинами. Рассчитывается, когда необходимо проанализировать обеспеченность населения врачами, больничными койками, лекарствами и т.д.
Вычисляется он по следующей формуле:
Абсолютный размер явления
–––––––––––––––––––––––––––––––––––––––––––––––– х 10 000
Абс. размер среды, не продуцирующей данного явления
Например: население Н-ской области составляет 2 780 341 человек. В крае функционирует 29 860 больничных коек. Рассчитать показатель обеспеченности койками:
на 2780341 чел. – 29860 коек
на 10000 чел. – х 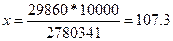 койки
койки
Сравнивая с подобными показателями страны, соседних регионов, нормативом потребности в стационарной помощи, можно сделать вывод о достаточности коечного фонда в Н-ской области.
Показатель наглядности – разновидность экстенсивного показателя. Рассчитывается, если нужно посмотреть, на сколько увеличивается или уменьшается какое-то явление. Характеризует отношение каждой из сравниваемых величин к исходному уровню, принятому за 100 или за 1. Этот показатель применяется для удобства сравнения, а также в тех случаях, когда необходимо показать направление процесса, тенденции (увеличение, уменьшение), не показывая уровня или размеров явления. Показатели наглядности можно рассчитывать, используя абсолютные величины, средние величины и, что чаще всего, относительные показатели.
Показатель наглядности рассчитывается с помощью обычной пропорции, когда одна из сравниваемых величин (чаще первая) принимается за 100% (это «базис»), а все остальные пересчитываются по отношению к исходной величине. Если в результате вычислений получается больше 100%, то отмечается наглядное увеличение, если меньше 100%, то – наглядное уменьшение изучаемого явления.
Например: вычислить показатели наглядности по следующему условию задачи:
| Годы | Показатели рождаемости в обл. (на 1000 населения) | Показатели наглядности |
| 17,6 | 100% | |
| 12,9 | 73,3% | |
| 8,7 | 49,4% | |
| 14,2 | 80,7% |
Расчет показателей наглядности:
17,6 – 100% 17,6 – 100%
12,9 – х 8,7 – х
12,9*100% 8,7*100%
в 1990 г. –––––––––– = 73,3% в 2000 г. –––––––– = 49,4%
17,6 17,6
17,6 – 100%
14,2 – х
14,2*100%
в 2010 г. –––––––––– = 80,7%
17,6
Вывод: анализ показателей наглядности говорит о тенденции снижения показателя рождаемости по сравнению с 1980 г.
Отсюда:
1) поиск причин этого явления;
2) реализация мероприятий по улучшению данного показателя.