При вращательном движении все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.
Областное государственное образовательное учреждение высшего профессионального образования
<<Астраханский инженерно - строительный институт>>
КАФЕДРА ЕСТЕСТВЕННОНАУЧНЧЫЙ ДИСЦИПЛИН
Отчет
По лабораторной работе № 1.4
<< ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА >>
Выполнил ст. группы СБ-14-13
Берсанов Б. Л.
Преподаватель (уч. ст., звание)
Соболева В.В
| дата | подпись | |
| допуск | ||
| результат | ||
| отчет |
Цель работы:
1. Изучить характеристики и основной закон динамики вращательного движения твёрдого тела.
2. Определить момент инерции крестообразного маятника (маятник Обербека).
3. Оценить момент тормозящей силы, действующий на тело в процессе вращения.
4. Определить момент инерции тела с учетом момента тормозящей силы.
5. Произвести расчет моментов, пользуясь энергетическими соотношениями.
Приборы и принадлежности:
1.Модульный учебный комплекс МУК-М1;
2.Блок секундомер электронный СЭ1;
3.Блок механический БМ1.
Контрольные вопросы:
1. Дать определение вращательного движения и всех величин, характеризующих данное движение?
2. Дать определение момента инерции материальной точки, системы материальных точек, твердого тела, центр масс?
3. Вывод момента инерции,сплошного однородного диска (цилиндра) относительно оси, перпендикулярной к плоскости диска и проходящей через его центр масс?
4. Физический смысл момента инерции твердого тела?
5. Получить расчетные формулы (31) и (44) для определения момента инерции?
6. Записать второй закон Ньютона для движения центра масс и основной закон динамики вращательного движения, дать определение всех величин, входящие в данные законы?
7. Сформулировать теорему Штейнера?
Ответы на контрольные вопросы:
При вращательном движении все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.
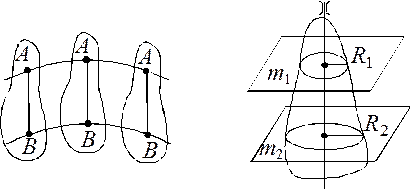
Рис. 1.
Виды механического движения: 1а) поступательного; б) вращательного.
Окружности, описываемые точками, находятся в плоскостях, перпендикулярных оси вращения (рис. 1б). Ось вращения может находиться как внутри тела, так и вне его.
Чтобы твёрдое тело с закреплённой осью привести во вращательное движение, необходимо хотя бы в одной из его точек приложить внешнюю силу 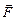 , не проходящую через ось вращения и непараллельную ей, другими словами, чтобы эта сила создавала момент силы.
, не проходящую через ось вращения и непараллельную ей, другими словами, чтобы эта сила создавала момент силы.
2. Центром масс(инерции) называют точку, масса которой равна массе всего тела, а положение определяется радиусом-вектором  :
:
Абсолютно твёрдым телом называют тело, расстояние между любыми двумя точками которого в условиях данной задачи можно считать постоянным.
Моментом инерции I материальной точки относительно некоторой оси называется скалярная величина, равная произведению массы материальной точки mi на квадрат расстояния ri от этой точки до оси вращения
Всякое твёрдое тело можно мысленно разбить на большое число частей, сколь угодно малых по сравнению с размерами всего тела, и рассматривать его как систему (совокупность) материальных точек, жёстко связанных друг с другом.
3. Используя формулу (9), можно рассчитать моменты инерции однородных тел правильной геометрической формы.
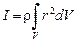 . .
| (9) |
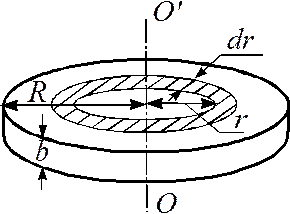
Рис. 2.
Сплошной однородный диск (цилиндр)
В качестве примера рассчитаем момент инерции сплошного однородного диска (цилиндра) относительно оси, перпендикулярной к плоскости диска и проходящей через его центр масс (рис 2). Разобьём диск на кольцевые слои толщиной dr. Обьём такого слоя равен dV = b·2πr·dr, где b – толщина диска. Подставим выражение для dV в уравнение 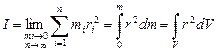 и вынесем постоянные за знак интеграла:
и вынесем постоянные за знак интеграла: 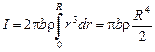 .
.
Учитывая, что произведение плотности диска ρ на его объём πR2b равно массе диска, получим:
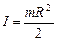 . .
| (10) |
4. Момент инерции I твёрдого тела относительно той же оси
 , ,
| (6) |
где mi и ri - масса i-той материальной точки и её расстояние до оси вращения.
5.
 . .
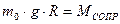
| (26) (30) |
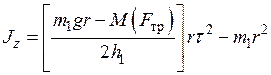 . .
| (28) |
Для определения момента инерции маятника I воспользуемся формулой (28), где величина МСОПР предварительно определена из измерений ε(m) и формулы (30). Подставив выражение ε из (26) и МСОПР из (30) в (28), получаем рабочую формулу для определения момента инерции маятника
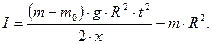
| (31) |
6. Второй закон Ньютона для движения центра масс твёрдого тела записывается в виде
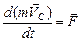 внешн внешн
| (2) |
где 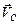 - скорость центра масс,
- скорость центра масс, 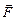 внешн - геометрическая сумма всех внешних сил, приложенных к телу.
внешн - геометрическая сумма всех внешних сил, приложенных к телу.
Основной закон динамики вращательного движения тела имеет вид
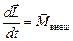 , ,
| (17) |
где 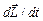 - производная по времени от момента импульса тела относительно произвольного неподвижного начала,
- производная по времени от момента импульса тела относительно произвольного неподвижного начала, 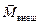 - геометрическая сумма моментов всех приложенных к телу внешних сил относительно того же начала.
- геометрическая сумма моментов всех приложенных к телу внешних сил относительно того же начала.
7. Теорема Штейнера. Момент инерции твёрдого тела относительно произвольной оси (I)равен сумме моментов инерции этого тела относительно оси, параллельной данной и проходящей через центр инерции I0 и произведения массы тела на квадрат расстояния между осями:
| I = I0 + md2, | (13) |
где m – масса тела; d – расстояние от центра масс до оси вращения.
Ход работы:Таблица. 1.
| № | m | MСОПР | t | r | I |
Таблица 2.