Порядок выполнения работы

Областное государственное образовательное учреждение высшего профессионального образования

<<Астраханский инженерно - строительный институт>>

 

 

КАФЕДРА ЕСТЕСТВЕННОНАУЧНЧЫЙ ДИСЦИПЛИН

Отчет

По лабораторной работе № 1.2

<< Изучение движения тела по наклонной плоскости >>

Выполнил ст. группы СБ-14-13

 

Берсанов Б. Л.

Преподаватель (уч. ст., звание)

 

Соболева В.В

дата подпись
допуск
результат
отчет

Цель работы:

1) изучить равномерное и равноускоренное движение тела по наклонной плоскости при наличии сил трения;

2) ознакомиться с одним из способов измерения коэффициента трения покоя и коэффициента трения скольжения;

3) проверить закон сохранения механической энергии при скатывании твердого тела с наклонной плоскости.

Приборы и принадлежности:

1) модульный учебный комплекс МУК-М2;

2) блок механический БМ2 (узел «плоскость»);

3) Блок секундомер электронный СЭ1.

Контрольные вопросы

1. Что называется силой трения. Объясните причины возникновения трения.

2. Какие существуют виды трения? От каких величин зависит сила трения.

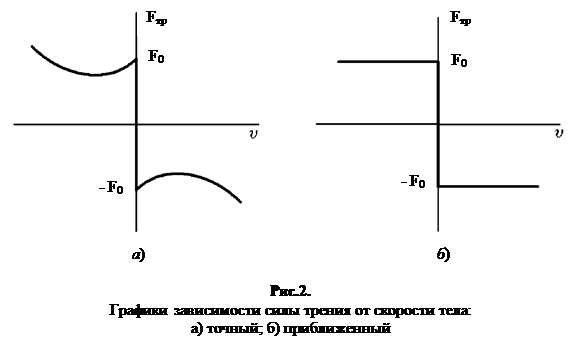
3. Объясните графики зависимости силы трения от скорости движения тела.

4. Как можно уменьшить силу трения.

5. Получить расчетные формулы (3) и (8) для определения коэффициентов трения покоя и скольжения.

6. При каком условии тело будет скатываться по наклонной плоскости без проскальзывания?

7. Как определить механическую энергию скатывающегося тела.

Ответы на контрольные вопросы:

1.Силой трения Fтр называется сила, возникающая при соприкосновении поверхностей двух тел и препятствующая их взаимному перемещению. Она приложена к телам вдоль поверхности их соприкосновения и направлена всегда противоположно относительной скорости перемещения.

 

2.Трение между поверхностями двух твердых тел при отсутствии какой-либо прослойки (например, смазки между ними) называется сухим.Трение между твердым телом и жидкой или газообразной средой называется вязким.

3.Если сила 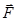превзойдет по величине 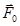, тело начинает скользить, причем его ускорение определяется результирующей двух сил: силой движения 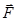и силы трения 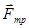, величина которой зависит от скорости скольжения. Характер этой зависимости определяется природой и состоянием трущихся поверхностей. Вид зависимости силы трения от скорости показан на рис.2 (по осям отложены проекции силы трения и скорости на направление, вдоль которых происходит скольжение). Данный график соответствует как случаю трения покоя, так и случаю скольжения. Вертикальным отрезком на графике показано изменение силы трения покоя от нуля до 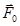(рис.2, а). При увеличении модуля скорости модуль силы трения сначала убывает, проходит через минимум, а затем начинает возрастать. В случае, когда состояние и природа поверхностей не изменяется и не требуется большая точность расчетов, силу трения скольжения можно считать практически не зависящей от скорости и равной максимальному значению силы трения покоя (рис.2, б).

Французские физики Г. Амонтон (1663-1705) и Ш. Кулон экспериментально установили, что сила трения 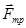пропорциональна силе нормального давления 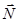, с которой одно тело действует на другое:

 

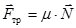. (1)

 

 

4.Уменьшить можно за счет нанесения смазки на трущиеся поверхности деталей, за счет улучшения шероховатости поверхностей.

 

5. а) 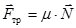. (1)

 

Постоянная μ называется коэффициентом трения и зависит от природы и состояния трущихся поверхностей. Если тело скользит по поверхности другого тела, то μ называют коэффициентом трения скольжения. Если же тела покоятся друг относительно друга, то его называют коэффициентом трения покоя μ0 (при Fтр=F0).


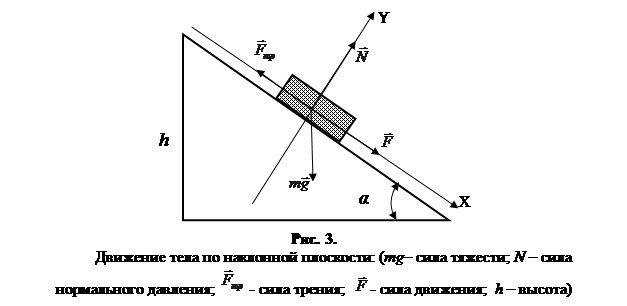
Для определения коэффициента трения покоя рассмотрим движение тела по наклонной плоскости высотой h (рис. 3). При медленном увеличении угла наклона плоскости можно найти такой угол α0, при котором брусок скачкообразно сдвинется с места и начнет скользить по плоскости.

 

В данном случае на брусок будут действовать три силы: сила тяжести 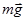, сила реакции опоры 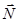и сила трения 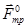. Выберем направление координатной оси X вдоль плоскости вниз, а координатной оси Y перпендикулярно плоскости вверх (рис.3). При отсутствии ускорения равнодействующая всех трех сил равна нулю. Запишем систему уравнений исходя из второго закона Ньютона:

 

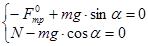(2)

 

Из системы уравнений (2) следует, что 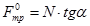. Исходя из выражения (1) можно получить

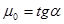(3).

 

б)Для определения коэффициента трения скольжения запишем уравнение динамики поступательного движения бруска в проекциях на оси OX и OY (рис.3):

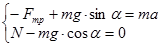(4)

 

Учитывая, что сила трения скольжения равна

 

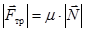, (5)

где μ – коэффициент трения скольжения. Решая систему уравнений (4) и (5) получаем:

(6)

Величину ускоренияа можно найти, измерив пройденный бруском путь S и соответствующее время t:

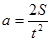. (7)

Формула (7) получена при скорости υ = 0, что соответствует условиям эксперимента. Подставляя формулу (7) в выражение (6), получаем:

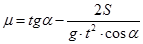(8)

 

 
 

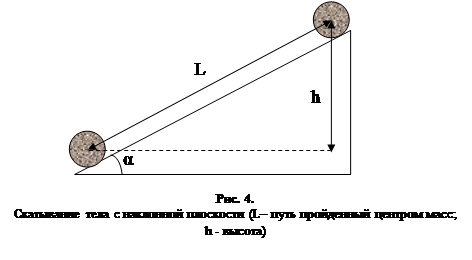6.Рассмотрим скатывающееся тело с наклонной плоскости (рис.4). Оно участвует в двух видах движений: поступательном движении центра масс О и вращательном движении относительно оси, проходящей через центр масс.

Скатывание тела без проскальзывания возможно при условии:

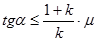, (9)

где μ – коэффициент трения скольжения тела о наклонную плоскость (коэффициент трения качения пренебрежимо мал); k – коэффициент, входящий в формулу момента инерции тела правильной геометрической формы относительно оси, проходящей через его центр масс (для диска k = 0,5, для шара k = 0,4, для обруча k = 1)

,

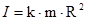где m – масса тела; R – радиус тела.

7.Поскольку сила трения качения мала, то полная механическая энергия скатывающегося тела постоянна. В начальный момент времени, когда тело покоится на вершине наклонной плоскости на высоте h, его полная механическая энергия равна потенциальной

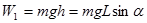, (10)

где L – путь, пройденный центром масс; α – угол наклона плоскости.

 

Порядок выполнения работы

Задание 1. Определение коэффициента трения покоя

1. Ослабив винт 2 (рис.5), установите плоскость под углом 0° к горизонту. Поместите брусок 4 (сталь-дерево) на наклонную плоскость в положении деревом вниз.

2. Медленно изменяя угол наклона плоскости найдите такой угол, при котором брусок скачком сдвинется с места и начнет скользить по плоскости. Запишите угол наклона плоскости α.

3. Вычислите по формуле (3) коэффициент трения покоя μ. Повторите опыт пятикратно.

4. Рассчитайте абсолютную и относительную погрешность коэффициента трения покоя.

5. Повторите п.п. 1-4, повернув брусок в положение сталью вниз.

6. Повторите п.п. 1-5 для второго бруска.

7. Сравните полученные в опыте значения коэффициентов трения покоя с табличными и с результатами измерения коэффициента трения скольжения.

 

Задание 2. Определение коэффициента трения скольжения

1. Ослабив винт 2 (рис.5), установите плоскость под углом 25° к горизонту, электромагнит при этом должен находиться в нижней части плоскости. Закрепите плоскость в таком положении, зажав винт 2.

2. Включите секундомер СЭ-1. Убедитесь, что он находится в режиме №1.

3. Поместите брусок с большей массой (сталь-дерево) на наклонную плоскость в положении деревом вниз, прижмите торец бруска, на который наклеена металлическая пластина, к электромагниту. Убедитесь, что брусок удерживается в этом положении.

4. Нажмите кнопку «Пуск» секундомера. При этом происходит одновременное отключение электромагнита и включение секундомера. Выключение секундомера происходит автоматически в момент удара бруска по финишному датчику.

5. Запишите время соскальзывания бруска t , пройденный бруском путь S , угол наклона плоскости α. Вычислите по формуле (8) коэффициент трения скольжения μ.

6. Повторите опыт пятикратно. Рассчитайте абсолютную и относительную погрешность коэффициента трения скольжения.

7. Повторите п.п. 3-6, повернув брусок в положение сталью вниз.

8. Повторите п.п.3-7 для других углов α.

9. Повторите п.п. 3-8 для второго бруска.

10. Сравните полученные в опыте значения коэффициентов трения скольжения с

табличными.

 

Задание 3. Скатывание твердого тела с наклонной плоскости

1. Ослабив винт 2 (рис.5), установите плоскость под некоторым углом α к горизонту. Поместите ролик 4 на наклонную плоскость.

2. Переключите тумблер управления электромагнитами механического блока в положение «плоскость».

3. Переведите секундомер СЭ1 в режим 1.

4. Нажмите кнопку «Пуск» секундомера. Измерьте время скатывания.

5. Повторите опыт не менее 5 раз.

6. Рассчитайте среднее значение времени.

7. Рассчитайте отклонение от среднего для каждого измерения времени и среднюю абсолютную погрешность измерений времени по формулам:

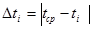и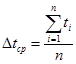

8. Вычислите значение механической энергии до, и после скатывания по формуле (11).

9. Повторите п.п. 1-8 для других углов наклона плоскости.

10. Повторите п.п. 1-9 для второго ролика.

11. Сделайте вывод о том, как меняется значение механической энергии в начальный и конечный момент времени при различных углах наклона плоскости.