Методика и решение.

Перечисленные в условии задачи параметры грузового фронта могут принимать разные значения, их сочетание является переменной величиной, влияющей на качественные и количественные показатели работы грузового фронта.

К таким показателям относятся: перерабатывающая способность грузового фронта, коэффициент использования ПРМ (относительная загрузка ПРМ); расходы, связанные с эксплуатацией грузового фронта или ПРМ, надежность работы ПРМ, время ожидания подачи вагонов на грузовой фронт и выполнения грузовых операций, а также связанные с ним расходы, численность работников и др.

По этой причине, данная задача относится к многокритериальным. Каждый критерий при заданных исходных условиях может иметь относительно “лучшие” или “худшие” значения. Будем считать “наилучшее” значение критерия условно оптимальным.

Известно, что невозможно найти такое сочетание значений оптимизируемых параметров, при котором все критерии одновременно принимали бы свои наилучшие или оптимальные значения.

Например, увеличение числа ПРМ позволяет увеличить перерабатывающую способность грузового фронта, но в то же время увеличить расходы связанные с их амортизацией и ремонтом; увеличение времени работы фронта в течение суток сокращает потребное число ПРМ и время ожидания выполнения грузовых операций, но увеличивает численность персонала и т.д.

Таким образом, задача сводится к нахождению такого набора значений варьируемых параметров, при котором их значения были бы максимально близки к оптимальным.

Для решения задачи используем метод Парето или метод “идеальной точки”. В качестве “идеальной точки” принимаем значение минимума суммы квадратов отклонений значений критериев от своих индивидуальных оптимальных значений:

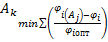(2.1)

Где - множество допустимых значений оптимизируемых параметров.

j – количество оптимизируемых параметров;

i – количество критериев оптимизации;

( ) – значение i – го критерия оптимизации при j – м наборе значений параметров;

отп – оптимальное значение i – го критерия при заданных исходных условиях.

Множество допустимых значений оптимизируемых параметров можно определить следующим образом:

Количество смен работы фронта в течение суток, .

Оно может изменяться от = 1 до = 3.

Количество подач вагонов на грузовой фронт, х.

Минимальное количество подач определяется из ограничения по длине грузового фронта по формуле:

(2.2)

Где - длина вагона, для расчета можно принять = 15 м.

Максимальное число подач рассчитывают из ограничения по ресурсу локомотиво-часов, которые можно использовать для подачи:

(2.3)

Количество ПРМ. z.

Минимальное число ПРМ определяют из условия переработки суточного грузопотока:

(2.4)

Где – коэффициент, учитывающий дополнительные операции, выполняемые ПРМ в зоне хранения, = 1,2;

- коэффициент неравномерности перевозок, ( = 1,1 1,3);

– время нахождения ПРМ в ремонте, = 10 15 суток.

При получении дробного значения оно округляется в большую сторону.

Максимальное число ПРМ определим из ограничения по величине инвестиций (2.5)

Величина округляется в меньшую сторону.

В качестве примера выполним расчёт оптимальных значений перечисленных выше параметров с использованием трех критериев:

1) Перерабатывающая способность грузового фронта -

2) Расходы на амортизацию и ремонт ПРМ -

3) Коэффициент загрузки грузового фронта -

Значения критериев определим по следующим формулам

(2.6)

(2.7)

Где A– норма отчислений на амортизацию и ремонт ПРМ (А=0,247 для электропогрузчиков; А=0,276 для автопогрузчиков; А=0,134 для козловых кранов;)

- нормативный коэффициент эффективности капитальных вложений,

(2.9)

Где – продолжительность технологических перерывов в работе фронта, ).

Допустимые значения параметров рассчитываются по формуле (2.2 – 2.5):

;

При

Расчёт значений критериев приведен в табл. 2.1.

В последней строке табл. 2.1 приведены наилучшие индивидуальные значения каждого критерия: т/сут, т.к. оптимальным значением перерабатывающей способности является максимально возможное, руб, т.к. оптимальным значением затрат является минимально возможное , т.к. оптимальное значение загрузки технических средств изменяются в пределах 0,75 - 0,8.

По последнему столбцу табл. 2.1 определяем оптимальное сочетание варьируемых параметров исходя из условия (2.1). Минимальная сумма квадратов отклонений критериев от своих оптимальных значений равна =0,447 что соответствует =3, x=3, z=3.

Следовательно, именно это сочетание значений варьируемых параметров является оптимальным. Однако, это решение оптимально только в том случае, если все критерии равноценны. На практике часто требуется оптимизировать параметры так, чтобы обеспечить определенную величину простоя вагонов, учесть ограничения по эксплуатационным расходам и т.д. , т.е. когда роли критериев различны. Относительно значимость каждого критерия для решения определенных задач можно учесть с помощью весовых коэффициентов.

Таблица 2.1