Простейшая задача вариационного исчисления.
Задача 1. Пусть 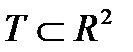 - открытая внутренняя область;
- открытая внутренняя область;  (точки множества
(точки множества  обозначим
обозначим 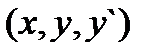 ),
), 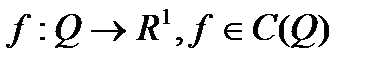 - заданная функция;
- заданная функция; 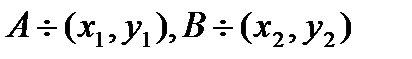 ,
,  - фиксирование точки,
- фиксирование точки,  . Функцию
. Функцию  назовем допустимой
назовем допустимой 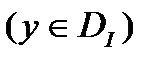 , если
, если  ,
, 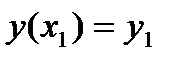 ,
, 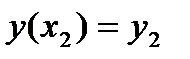 ,
, 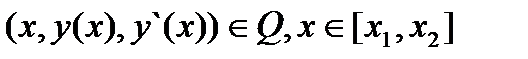 . Каждой
. Каждой  поставим в соответствие действительное число
поставим в соответствие действительное число  . Требуется определить min функционала I на множестве
. Требуется определить min функционала I на множестве 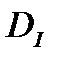 .
.
Задача 1 – простейшая вариационная задача.
Замечание:  ,
, 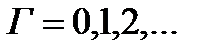 множество всех определённых на
множество всех определённых на 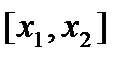 функций, имеющих производные до r порядка включительно, которая допускает разрывы первого рода в конечном числе точек и имеет в них одностороннюю непрерывность.
функций, имеющих производные до r порядка включительно, которая допускает разрывы первого рода в конечном числе точек и имеет в них одностороннюю непрерывность.
Краткая запись задачи 1:  ,
, 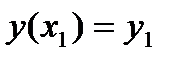 ,
, 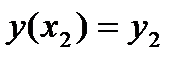 .
.
Замечание2 Если в  определить норму так:
определить норму так:
1) 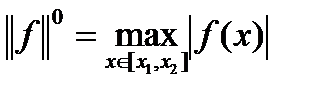 , 2)
, 2) 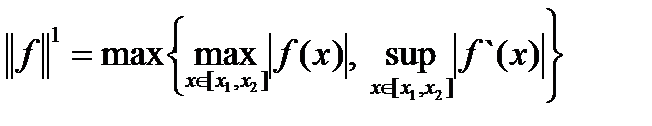 , а расстояние
, а расстояние
2) 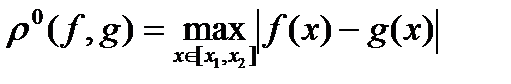 и 2)
и 2)  , то можно вести речь о сильном и слабом локальном минимуме.
, то можно вести речь о сильном и слабом локальном минимуме.
Опр1 Локальный минимум в задаче1 сильный (слабый), если окрестность, фигурирующая в его определении задаётся с помощью расстояния нулевого ( 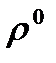 ) или (первого (
) или (первого ( 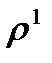 )) порядка.
)) порядка.
Теорема1(необходимые условия локального минимума 1 порядка). Пусть  и
и  доставляет локальный минимум в задаче1. Тогда
доставляет локальный минимум в задаче1. Тогда 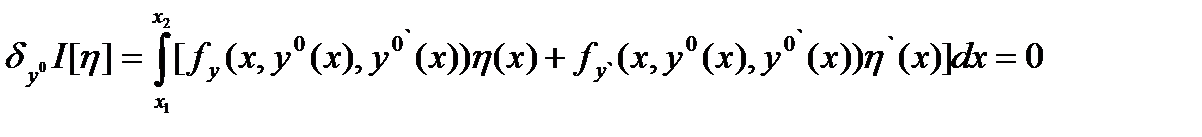
 .
.