Данные для построения кривой безразличия
| Набор | Qy (яблоки) | Qx (бананы) |
| М1 | ||
| М2 | ||
| М3 | ||
| М4 |
Выделяют следующие свойства кривых безразличия:
Свойство 1. Кривые безразличия имеют отрицательный наклон.
Допустим, что человек потребляет недельный набор М3, который состоит из 3 яблок (товар Y) и 6 бананов (товар X) в неделю (Рис. 6).
 |
Возможно потребитель пожелает отказаться от 1 яблока, но в соответствии с предложением III ординалистической теории полезности "больше – лучше, чем меньше", набор М5, состоящий из 2 яблок и 6 бананов, даст меньшую полезность, чем набор М3 (Рис.7).
Карта кривых безразличия – графическое описание предпочтений человека. Кривая безразличия может быть нарисована для любого набора на графике. Кривые безразличия, более удаленные от начала координат, соответствуют более высоким уровням полезности. На графике U1<U2<U3<U4.
 |
Поэтому М5 не может быть на той же самой кривой безразличия. что и М1. Чтобы обеспечить себе большую полезность, то есть иметь полезность на уровне набора М3 уменьшение качества потребляемых за неделю яблок должно быть компенсировано добавлением некоторого качества бананов. Графически это означает остаться на данной кривой безразличия, уменьшение товара Y на любую величину - ΔQy должно быть заменено дополнительным количеством товара X+ΔQX. Таким образом, наклон кривых безразличия (ΔQY / ΔQX) всегда будет отрицательным, так как числитель и знаменатель всегда будут иметь противоположный знак (Рис.8)
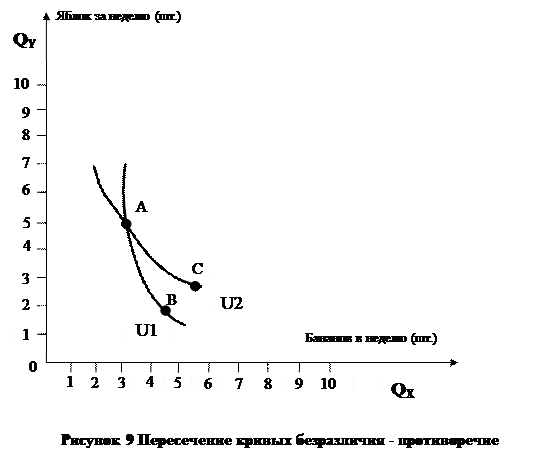 |
Свойство 2. Две кривые безразличия не могут пересекаться. Экономисты исходят из предположения о возможности пересечения кривых безразличия, показанных на рис.9
Если набор, представленный точкой А, был бы характерен для обеих кривых U1 и U2, где U2> U1, это означало бы, что потребитель не делает различия между А и В, а также между А и С. Отсюда следует, что он не делает различия между В С. Однако набор В содержит меньшее количество X и Y, чем набор С. Из этого должно следовать, что он предпочитает набор С набору В. Это противоречие, поскольку он не может одновременно предпочитать один набор другому и не делать различия между ними.
Тогда (по определению кривой безразличия – линии равных полезностей),
В ~ А, С ~ А.
Согласно предположения II (транзитивности)
В ~ С,
но этого не может быть, так как по предположению III
В 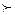 С.
С.
Таким образом, две кривые безразличия не могут иметь общую точку, так как один набор товаров не может характеризоваться двумя различными уровнями полезности.
Свойство 3. Кривая безразличия может быть проведена через каждую точку в пространстве товаров (согласно предположению о сравнимости). Таким образом, экономисты изображают множество кривых безразличия – карту безразличия (Рис.7)
Свойство 4. Предельная норма замещения уменьшается при движении вдоль кривых безразличия. Кривые безразличия выпуклы к началу координат.
Под предельной нормой замещения Y на X (MRS[13]XY) экономисты понимают количество товара Y, от которого потребитель отказался бы, чтобы получить еще одну единицу товара X, сохраняя общую полезность товарного набора (оставаясь на данной кривой безразличия).
Предельная норма замещения определяется как положительное количество товара Y, от которого потребитель желает отказаться ради дополнительной единицы X
 |
Предельная норма замещения измеряет желание потребителя обменять один товар (Y) на каждую единицу другого товара (X), при этом не приобретая и не теряя полезность. Кривизна кривой безразличия изображенной на рис. 8 показывает, что количество Y, от которого потребитель хочет отказаться ради еще одной единицы X, уменьшается по мере увеличения количества X, замещающего Y в наборе.
Экономисты исходят из того, что потребитель остается на одно и той же кривой безразличия, если не теряет и не приобретает полезности при отказе от потребления некоторого количества товара Y (ΔQY), чтобы получить еще одну единицу товара X (ΔQX=1).
Количество товара Y, которое будет обменено на единицу товара X, между любыми двумя точками на кривой может быть записано как (ΔQY/ΔQX). Это наклон кривой безразличия, который показывает готовность потребителя отказаться от единиц товара Y для получения единиц товара X. Но наклон кривой безразличия отрицателен. Такой подход к рассмотрению MRSXY приводит к получению отрицательного числа. Поэтому предельная норма замещения это произведение наклона кривой безразличия и –1.
Кривизна кривой безразличия на рис.8 отражает уменьшающиеся предельные нормы замещения Y на X. Предельная норма замещения между точками М1 и М2 равна 4. Это количество Y , от которого потребитель отказался бы ради дополнительной единицы X. Предельная норма замещения равная 4, означает, что потребитель был бы готов отказаться от 4 яблок в неделю, чтобы получить на один банан больше, оставаясь на данной кривой безразличия. MRSXY=4 при потребительском наборе, содержащем 10 яблок и 4 банана в неделю (набор М1).
Далее предполагают, что потребитель обладает набором, представленным точкой М2. У него появилось желание отказаться только от 3 яблок в обмен на еще один банан в неделю, оставаясь на той же кривой безразличия. Предельная норма замещения уменьшилась, когда потребитель перешел от набора М1 к набору М2, так как кривая безразличия становится более пологой по мере того, как X замещает Y вдоль кривой. Выпуклая форма кривой безразличия (по отношению к началу координат) означает, что по мере уменьшения яблок и увеличения бананов в наборе количество яблок, которое потребитель хочет обменять на дополнительное число бананов, уменьшается. Имея недельный набор М3 (3 яблока и 6 бананов) потребитель желал бы отказаться только от двух яблок, чтобы получить еще один банан в недельном наборе. В таблице 6 обобщены данные для вычисления MRSXY в различных точках кривой безразличия
Таблица 6
Предельная норма замещения Y на X (MRSXY)
| Набор | QY | QX | MRSXY | |
| М1 | 4 ед. Y за 1 ед. X | |||
| М2 | ||||
| 3 ед. Y за 1 ед. X | ||||
| М3 | ||||
| 2 ед. Y за 1 ед. X | ||||
| М4 |
Таким образом, ординалистическая теория предельной полезности описывает систему предпочтений потребителя.