Точно также

если А 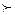В и В ~ С,

или А ~ В и В 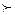С,

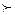то А С,

а также

если А ~ В и В ~ С,

то А ~ С.

Справедливость первого и второго предположений в рамках простого "здравого смысла" обеспечивает возможность упорядочения потребителем всего множества товарных наборов и присвоения полезностям этих наборов численных значений.

3. Предположение о ненасыщаемости. Это допущение, соответствует интуитивному представлению о том, что "больше – лучшем меньше". Если набор А содержит не меньшее количество единиц каждого товара, чем набор В, то набор А предпочтительнее или безразличен набору В. Если же набор А содержит при этом большее количество единиц хотя бы одного товара, чем набор В, то набор А предпочтительнее набора В.

Однако, некоторые продукты, которые люди менее всего предпочитают называются "экономическим антиблагом". Примеры экономического антиблага (антитовара) – мусор, загрязненная вода.

В данной теории предполагается, что полезность лишь порядково измерима. Функция порядковой полезности позволяет судить о том, какой из наборов предпочтительнее и не дает возможности оценивать и сравнивать разницу в полезности наборов (насколько один набор предпочтительнее другого).

Функция полезности это отношение между объемами потребляемых товаров и услуг и уровнем полезности (удовлетворенности), достигаемым потребителем. Функция полезности – способ представления предпочтений человека. Она может быть представлена в следующем виде:

U = f (Q_x, Q_y),

где f – символ функции, показывающий, что U (уровень полезности) зависит от переменных в скобках. Функция полезности предполагает, что полезность получаемая человеком, зависит только от количеств товаров X(Q_x) и Y(Q_Y), потребляемых за определенный период, например, неделю. Упрощенная функция полезности в уравнении концентрируется на основных факторах, влияющих на потребительский выбор и объясняет выбор количеств только двух товаров. Основные выводы, полученные для двух товаров верны и на случай множества товаров.

Основная идея графического представления системы предпочтений (функции полезности) потребителя с помощью кривых безразличия (впервые примененных английским экономистом Ф. Эджуортом в 1881 г.) состояла в следующем: соединить все точки характеризующие наборы товаров, имеющие некоторый определенный уровень полезности. При этом потребителю безразлично, какой из этих наборов выбирать. Полученную линию равной полезности называют кривой безразличия. Соединив все точки характеризующие наборы товаров и имеющие некоторый иной уровень полезности (U₂) получают другую кривую безразличия. Выполнив эти действия со всеми возможными наборами товаров, получают карту безразличия – множество кривых безразличия, соответствующих всем возможным уровням полезности для данного потребителя. Карта безразличия это графическое изображение шкалы предпочтений потребителя.

Рассмотрим пример, когда потребитель располагает фиксированным денежным доходом, который он полностью тратит на потребление. Для простоты предполагают, что он покупает только два товара, X и Y. X – это бананы, Y – яблоки. Потребительская корзина – комбинация, набор X и Y для недельного потребления. Символ Q_x это количество бананов в наборе, Q_y – количество яблок.

На рис. 6 точка М1 представляет набор, состоящий из 4 бананов и 10 яблок в неделю. Кривая безразличия изображает совокупность наборов, между которыми потребитель не делает различия. Любой набор на кривой обеспечит один и тот же уровень удовлетворения, что и начальный набор М1. Потребитель не делает различия между набором М1 из 4 бананов и 10 яблок и набором М2 из 5 бананов и 6 яблок, а также между наборами М3

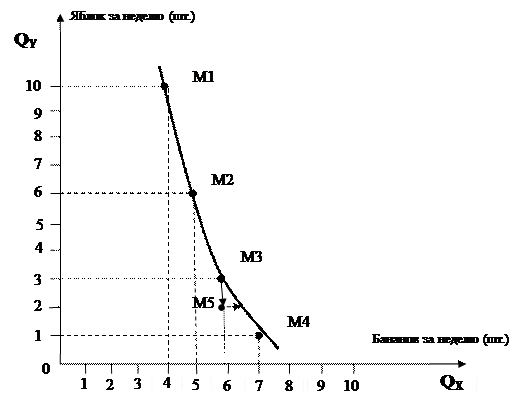из 6 бананов и 3 яблок и М4 из 7 бананов и одного яблока.

Каждая точка на кривой безразличия отображает рыночный набор ("потребительскую корзину") товаров. Потребитель не делает различия между всеми наборами, расположенными на кривой.

В таблице 5 представлены данные, на базе которых строится кривая безразличия.

Таблица 5