Главный момент сил инерции твердого тела, вращающегося вокруг неподвижной оси
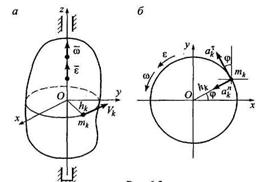Вычислим координаты главного момента сил инерции твердого тела, вращающегося вокруг неподвижной оси. Ось Oz совместим с осью вращения, а оси Ох и Оу скрепим с вращающимся телом, тогда 
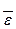(0,0,ε) и 
(0,0,ω), rk(xk;yk;zk) - радиус-вектор рассматриваемой точки тк. При вращении тела вокруг неподвижной оси Oz ускорение любой точки тк состоит из нормального ускорения 
и касательного ускорения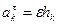 
, где hk - расстояние точки k от оси вращения Oz:
;
;
.
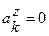Здесь учтено, что hkcosφ = xk , hksinφ = ук, хк и ук - координаты точки тк.
Тогда, согласно (6.12), получим,
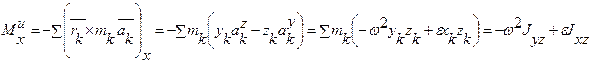
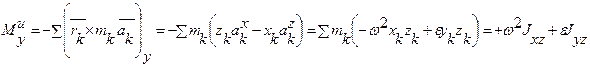
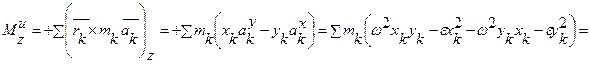
Здесь Jxz, Jyz - центробежные моменты инерции, Jz - осевой момент инерции.
Таким образом, главный момент сил инерции твердого тела, вращающегося вокруг неподвижной оси, сводится к паре сил, момент которой равен
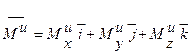
где
, 
, 
Если ось вращения проходит через центр тяжести тела и оси Oxyz являются главными осями, то
, 
,
Пример 3. Через блок весом Mg и радиусом R перекинута нерастяжимая нить, на конце которой подвешен груз А весом mg. Определить ускорение а груза А, натяжение нити Т и давление на подшипник оси блока.
Решение. Пусть груз А опускается вниз, тогда сила инерции груза вверх: Fи = ma.
Поскольку ось вращения диска является осью симметрии, то Jxz=Jyz = 0. Следовательно, момент от сил инерции, равен и направлен в сторону противоположную вращению диска.
Отбросим опору О, заменим ее действие реакциями подшипника Rx и Ry. Составим уравнения кинетостатики:
, 
;
, 
;
, 
.
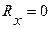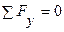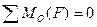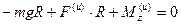Подставим в последнее уравнение значения силы инерции F(u)=ma и момента от сил инерции = (J/R)a, где t = a/R, и решим его относительно ускорения а.
Получим
, 
.
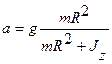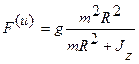Тогда из первых двух уравнений (а) определим
, 
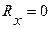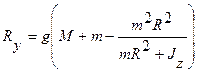
Для определения натяжения нити разорвем гибкую связь и заменим ее действие натяжением Т. Добавляя внешнюю силу mg и силу инерции F(и), имеем
-mg+F(u)+T = 0,
откуда T = mg- F(и) = m(g - а) =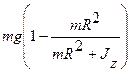 
.
Если считать диск сплошным телом, то Jz - —mR2, тогда
, 
, 
, 
.
Лекция 16 (Аналитическая механика)
«Связи и их классификация. Обобщенные координаты,
Работа силы на возможном перемещении»
В основу классической механики положены понятия пространства, времени, силы и массы. Она оперирует векторными величинами, векторными уравнениями и их проекциями на координатные оси. Аналитическая механика построена на основных принципах, основанных на сравнении движений. Этот принцип изучает мгновенное состояние движения и возможные отклонения от этого состояния, допускаемые связям в данный момент времени. В аналитической механике широко применяются скалярные меры движении материальных объектов и меры их действия (кинетическая энергия, работа сил и т.д.).
Основы изложения аналитической механики составляют некоторые общие принципы, из которых аналитическим путем получаются дифференциальные законы движения на основе которых изучается движение твердых тел и системы материальных точек.