Секторная скорость, теорема площадей
Секторной скоростью точки 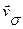 или
или  относительно центра О называют векторную величину, определяемую по формуле
относительно центра О называют векторную величину, определяемую по формуле 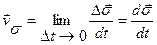
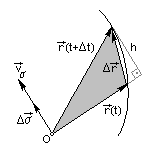
|  -вектор, численно равный заштрихованной на рисунке площади, заметаемой радиус-вектором -вектор, численно равный заштрихованной на рисунке площади, заметаемой радиус-вектором 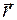 движущейся точки за время Dt, направление вектора движущейся точки за время Dt, направление вектора 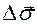 берется перпендикулярно плоскости движения по правилу правого винта. Секторная скорость перпендикулярна плоскости движения и приложена в точке, относительно которой она вычисляется. берется перпендикулярно плоскости движения по правилу правого винта. Секторная скорость перпендикулярна плоскости движения и приложена в точке, относительно которой она вычисляется.

|
Тогда 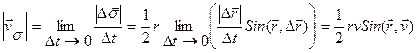 ,
,
то есть 
Направление вектора 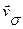 также соответствует правилу векторного произведения, так что
также соответствует правилу векторного произведения, так что

Согласно этому теорему об изменении кинетического момента точки можно записать в виде:

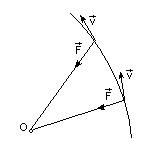
| Центральной называют силу, действующую на точку, линия действия которой при движении точки все время проходит через некоторую неподвижную точку – центр силы. Центр силы может быть как притягивающим, так и отталкивающим.
Для центральной силы ее момент относительно ее центра всегда равен нулю и
 
|
В проекциях на декартовы оси координат имеем:

здесь С1,С2,С3 – константы.
Умножая первое соотношение на x, второе – на y, третье – на z и складывая, получим:
С1x+С2y+С3z=0;
то есть координаты движущейся точки x,y,z удовлетворяют уравнению плоскости, проходящей через начало координат О.
Траектория точки, движущейся под действием центральной силы, является плоской кривой, лежащей в неподвижной плоскости, проходящей через центр силы.
Так как  , то
, то 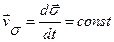 и
и
 или
или  .
.
Эта формула выражает интеграл площадей: при движении точки под действием центральной силы секторная скорость является постоянной величиной и, следовательно, заметаемая радиус-вектором площадь пропорциональна времени.
Сравним это со вторым законом Кеплера: «Секторная скорость каждой планеты относительно Солнца постоянна».
Дифференциальные уравнения плоского движения твердого тела

|
Рассмотрим систему отсчета S’, связанную с центром масс материальной системы, оси (x’y’z’) этой системы параллельны осям системы S (Oxyz). Система отсчета S’ называется системой отсчета Кенига.
Для любой точки материальной системы справедливо соотношение 
|
Для поступательного движения системы точек имеем для скоростей точек :  , при этом (
, при этом ( , т.к. система S’ не вращается и всегда движется поступательно).
, т.к. система S’ не вращается и всегда движется поступательно).
Составим выражение для кинетического момента системы точек и подставим в него выражение для  :
:
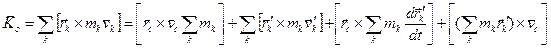
По определению положения центра масс в системе S’ 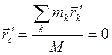 и последних два слагаемых обращаются в ноль (предпоследнее обращается в ноль в силу
и последних два слагаемых обращаются в ноль (предпоследнее обращается в ноль в силу  ).
).
Окончательно 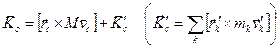 , то есть кинетический момент абсолютного движения системы относительно неподвижной точки О равен векторной сумме кинетического момента центра масс относительно этой же точки, как если бы в центре масс была сосредоточена вся масса системы, и кинетического момента системы
, то есть кинетический момент абсолютного движения системы относительно неподвижной точки О равен векторной сумме кинетического момента центра масс относительно этой же точки, как если бы в центре масс была сосредоточена вся масса системы, и кинетического момента системы  относительно центра масс для относительного движения системы по отношению к подвижной системе координат S’, движущейся поступательно вместе с центром масс.
относительно центра масс для относительного движения системы по отношению к подвижной системе координат S’, движущейся поступательно вместе с центром масс.
Теорема об изменении кинетического момента:  .
.
Подставляя сюда ранее полученные выражения для 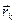 и
и  , после преобразований получим:
, после преобразований получим:

Перенося из правой части в левую первое слагаемое и учитывая, что 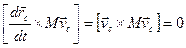 имеем
имеем
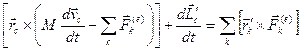
Выражение в круглых скобках равно нулю на основании теоремы о движении центра масс. Тогда

Это теорема об изменении кинетического момента системы относительно центра масс для относительного движения системы по отношению к системе, движущейся поступательно с центром масс, она формулируется также, как если бы центр масс был неподвижной точкой.

| Используя теорему о движении центра масс и изменении кинетического момента системы относительно центра масс для относительного движения системы по отношению к системе S’, движущейся поступательно вместе с центром масс, получим три дифференциальных уравнения плоского движения твердого тела:

|
Первые два уравнения являются дифференциальными уравнениями движения центра масс в плоскости Oxy, третье уравнение – дифференциальное уравнение вращения тела относительно центра масс.
Лекция 14 (динамика)
«Теорема об изменении кинетической энергии, закон сохранения механической энергии»
Теорема об изменении кинетической энергии

| Работа силы. Элементарная работа силы равна скалярному произведению силы на дифференциал радиус-вектора точки приложения силы.
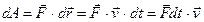 Элементарная работа силы равна также скалярному произведению элементарного импульса силы на скорость точки.
Элементарная работа силы равна также скалярному произведению элементарного импульса силы на скорость точки.

|
Если сила Fперпендикулярна приращению радиус-вектора dr, то элементарная работа силы равна нулю.
Полная работа силы 
Другое определение:  , где t=0 соответствует положению М0, а момент времени t – положению М.
, где t=0 соответствует положению М0, а момент времени t – положению М.
Последняя формула удобна для вычисления работы силы, когда сила известна как функция времени.
Размерность работы [A]=1Дж=1Н×м
Мощность. Мощность силы или работоспособность какого-либо источника силы часто оценивают той работой, которую он может совершить за единицу времени.
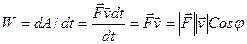
Размерность мощности [W]=1Вт=1Дж/с.
Работа силы тяжести.
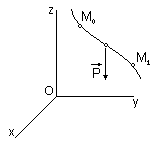
| Px=0, Py=0, Pz= - mg

|
Для системы точек для каждой точки работа Ai=mig(z0i-z1i), полная работа
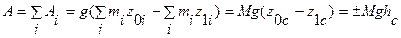
Работа линейной силы упругости.
Линейная сила упругости действует по закону Гука 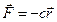 , где r – расстояние от точки равновесия, где сила равна нулю, до рассматриваемой точки М, с – постоянный коэффициент жесткости. Выберем начало координат в точке равновесия, тогда работа
, где r – расстояние от точки равновесия, где сила равна нулю, до рассматриваемой точки М, с – постоянный коэффициент жесткости. Выберем начало координат в точке равновесия, тогда работа
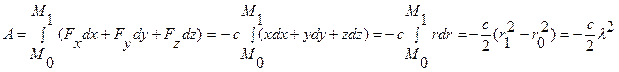 ,
,
где l - деформация (удлинение) пружины.
Работа силы, приложенной к твердому телу.

| При поступательном движении 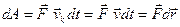 При вращении твердого тела вокруг неподвижной оси
При вращении твердого тела вокруг неподвижной оси
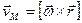
 (при выводе последнего соотношения мы использовали свойство смешанного векторно-скалярного произведения)
(при выводе последнего соотношения мы использовали свойство смешанного векторно-скалярного произведения)
|
Полная работа 
Для свободного тела.

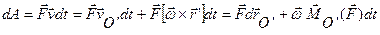 Элементарная работа силы, приложенной к какой-либо точке твердого тела, в общем случае движения складывается из элементарной работы на элементарном поступательном перемещении вместе с какой-либо точкой тела (полюсом) и на элементарном вращательном перемещении вокруг этой точки.
Элементарная работа силы, приложенной к какой-либо точке твердого тела, в общем случае движения складывается из элементарной работы на элементарном поступательном перемещении вместе с какой-либо точкой тела (полюсом) и на элементарном вращательном перемещении вокруг этой точки.
|
Кинетическая энергия.
Кинетической энергией Т материальной точки называют ½ произведения массы точки на V2: T=½ mv2. Размерность кинетической энергии - 1Дж=1Н м
Кинетической энергией системы Т называют сумму кинетических энергий всех точек механической системы, то есть

Теорема Кенига. Разложим движение механической системы на переносное поступательное вместе с центром масс и относительное по отношению к системе координат, движущейся поступательно вместе с центром масс (оси Кенига из параграфа «Дифференциальные уравнения плоского движения твердого тела»).
Запишем связь координат и скоростей точек системы в абсолютной (неподвижной) и подвижной системе отсчета:

Выражение для кинетической энергии системы может быть представлено в следующем виде:
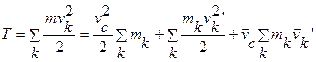 ;
;
В силу того, что начало подвижной системы отсчета совмещено с центром масс системы точек  и третье слагаемое в предыдущей формуле обращается в ноль (выражение в круглых скобках в системе отсчета, связанной с центром масс, равно нулю).
и третье слагаемое в предыдущей формуле обращается в ноль (выражение в круглых скобках в системе отсчета, связанной с центром масс, равно нулю).
В итоге получаем: 
Это означает, что кинетическая энергия системы в абсолютном движении складывается из кинетической энергии центра масс, как если бы в нем была сосредоточена вся масса системы, и кинетической энергии системы относительно центра масс.
Примеры:
1. Кинетическая энергия твердого тела при поступательном движении - 
2. Кинетическая энергия твердого тела при вращении вокруг неподвижной оси –

3. Кинетическая энергия твердого тела при плоском движении - 
Теорема об изменении кинетической энергии точки
Умножим скалярно второй закон Ньютона на 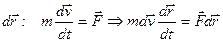
После несложных преобразований получим:

или 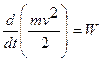 ;
;
также 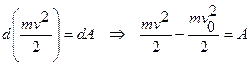
то есть изменение кинетической энергии точки на каком-либо перемещении равно работе силы, действующей на точку на том же перемещении.
Теорема об изменении кинетической энергии системы материальных точек
Для каждой точки системы имеем: 
Здесь мы выразили равнодействующую силу для точки mk в виде суммы равнодействующих внешних и внутренних сил, действующих на точку.
Проводя суммирование и вынося знак дифференциала за знак суммы, будем иметь:
 или
или 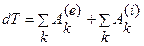
Получили закон изменения кинетической энергии для системы точек: «изменение кинетической энергии системы точек равно работе все внутренних и внешних сил на всех перемещениях всех точек». Работа внутренних сил не равна нулю, поскольку под действием одинаковых сил действия и противодействия точки разной массы имеют различные перемещения и работа внутренних сил полностью не компенсируется.
Проведем интегрирование между начальным и конечным положением системы, тогда будем иметь:
 или
или 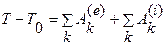
Имеем теорему в конечной форме: «изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему, на соответствующих перемещениях точек при том же изменении положения системы».
Для твердого тела  и
и 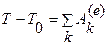
Потенциальное силовое поле и потенциальная энергия
Силовым полем называют часть пространства, в каждой точке которого на материальную точку действует определенная сила, зависящая от координат точки и времени (стационарный и нестационарный случаи).
Силовое поле называют потенциальным, если имеется силовая функция 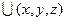 , такая, что
, такая, что 
Силовая функция определяется с точностью до постоянной, так как добавка в виде константы под знак частной производной не влияет на значения Fx, Fy, Fz.
Запишем работу силы потенциального силового поля:

Элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функции.
Полная работа силы  на участке от положения М0 до положения М равна
на участке от положения М0 до положения М равна

Эта работа не зависит от формы траектории, работа силы в потенциальном силовом поле по замкнутой траектории равна нулю.
Можно показать, что необходимым и достаточным условием того, что силовое поле является потенциальным, является условие 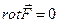 , то есть поле безвихревое.
, то есть поле безвихревое.
Непотенциальными являются силы сопротивления, зависящие от скорости и силы трения. Сила сухого трения скольжения не будет потенциальной, так как хотя она постоянна и не зависит от скорости, но направление силы трения от скорости зависит.
Наряду с силовой функцией можно ввести другую функцию, характеризующую запас энергии в данной точке поля – потенциальную энергию.
Потенциальной энергией Pматериальной точки в рассматриваемой точке силового поля M называют работу, которую совершают силы поля, действующие на материальную точку при перемещении ее из положения M в начальное положение M0:
 .
.
Постоянная С0 одна и та же для всех точек поля, зависящая от того, какая точка поля была выбрана за начало отсчета.
В конечном итоге имеем: 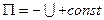 , то есть силовая функция и потенциальная энергия отличаются знаком о определены с точностью до постоянной.
, то есть силовая функция и потенциальная энергия отличаются знаком о определены с точностью до постоянной.
Закон сохранения механической энергии
Для материальной точки ранее имели:  .
.
Если материальная точка движется в стационарном потенциальном силовом поле, то A=P0 - P, то есть

При движении точки в стационарном потенциальном силовом поле ее полная механическая энергия, равная сумме кинетической и потенциальной энергий, остается постоянной величиной. Это и является формулировкой закона сохранения полной механической энергии.
Для системы точек в стационарном потенциальном силовом поле
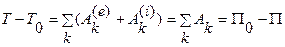
Здесь P - потенциальная энергия внутренних и внешних сил, действующих на точки системы. Отсюда
T-T0=P0 - P или T+P=T0+P0=E=E0,
то есть полная механическая энергия при движении системы в стационарном силовом поле внешних и внутренних сил является постоянной величиной.
Для твердого тела P - потенциальная энергия внешних сил, так как потенциальная энергия внутренних сил постоянна и может быть положена равной нулю. Для изменяемой механической системы учитываем потенциальную энергию и внутренних сил.
Если для системы выполняется закон сохранения механической энергии, то она называется консервативной.
Диссипативные силы характерны тем, что приводят к уменьшению механической энергии E (переводя ее в тепло).
Лекция 15 (Аналитическая механика)
«Принцип Даламбера, главный момент и главный вектор сил инерции»
Н аряду с рассмотренными методами изучения движения точки и механической системы, основанными на законах классической механики, применяется метод кинетостатики или принцип Д'Аламбера.