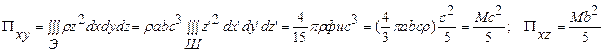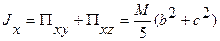Внутренними силами материальной системы называют силы взаимодействия между точками рассматриваемой системы, мы их будем обозначать .

Механической системой называется любая совокупность материальных точек.

Внешними силами материальной системы называются силы, с которыми действуют на точки системы тела и точки, не входящие в рассматриваемую систему, будем их обозначать .

Простейшие свойства внутренних сил системы

Внутренние и внешние силы могут включать в себя как активные силы, так и реакции связей.

Пусть система состоит из n точек. Тогда по третьему закону Ньютона, например для точек 1 и 2, внутренние силы взаимодействия этих точек равны по величине и противоположны по направлению:

Равнодействующая внутренних сил состоит из векторной суммы сил действия и противодействия, которая равна нулю: .

Если рассмотреть сумму моментов сил и относительно некоторой произвольной точки О, то легко видеть, что

т.к. обе силы имеют одинаковые плечи h и противоположные направления векторных моментов. Главный момент внутренних сил относительно точки О состоит из векторной суммы этих моментов внутренних сил:

Дифференциальные уравнения движения системы

Если к каждой точке системы приложить равнодействующую силу внешних сил и равнодействующую силу всех внутренних сил , то для любой к-ой точки системы можно составить дифференциальное уравнение движения в виде второго закона Ньютона:

Систему этих уравнений называют дифференциальными уравнениями движения механической системы в векторной форме. Если спроектировать их на оси координат, то получим 3n скалярных дифференциальных уравнения.

Мы видели, с какими трудностями приходится сталкиваться при интегрировании дифференциального уравнения движения точки, если сила зависит от времени, положения или скорости. Здесь же мы имеем систему уравнений и трудности неизмеримо возрастают. Поэтому особую роль в динамике системы материальных точек играют общие теоремы, позволяющие в отдельных случаях получить информацию о характере движения системы не проводя трудоемкого интегрирования системы дифференциальных уравнений.

Лекция 12 (динамика)

«Геометрические характеристики системы материальных точек.

Общие теоремы динамики системы точек»

Геометрические характеристики системы материальных точек.

Моменты инерции. Теорема Штейнера. Эллипсоид инерции.

Рассмотрим точку О, прямую L и плоскость В, а также точки материальной системы (одна из них A_i с массой m_i). Расстояния от точки A_i до точки О, прямой L и плоскости В обозначим через r_i, D_i и d_i соответственно.

Можно составить выражения:

Суммирование распространено по всем точкам материальной системы. Эти выражения называются моментами инерции соответственно относительно плоскости В, прямой L и точки О.

Аналитические выражения моментов инерции относительно основных координатных элементов связаны равенствами:

J_z=P_xz+P_zy, m=P_zx+P_zy+P_xy

(Момент инерции относительно какой-либо оси равен сумме моментов инерции относительно двух ортогональных плоскостей, проходящих через эту ось. Момент инерции относительно точки равен сумме моментов инерции относительно трех ортогональных плоскостей, пересекающихся в этой точке.)

Для сплошных тел суммы перейдут в интегралы:

Пример 1.

Для шара массы m, радиуса R (плотность

) имеем момент инерции шарового слоя текущего радиуса r толщины dr относительно центра:

, а для всего шара

поскольку

Теорема Штейнера

Проведем через центр масс материальной системы с координатами a,b,c оси x’,y’,z’ параллельно осям x,y,z. Тогда для любой точки системы x_i=x_i’+a, y_i=y_i’+b и момент инеции системы относительно оси z равен

Второе и третье слагаемое равны нулю в силу того, что в системе отсчета, связанной с центром масс, , а в четвертом слагаемом a²+b²=d² (d – расстояние между осями z и z’). Первое слагаемое есть момент инерции системы относительно оси z’. Окончательно имеем:

,

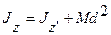то есть момент инерции относительно какой-либо оси z равен моменту инерции относительно параллельной и проходящей через центр масс оси z’ плюс Md², где d – расстояние между осями.

Следствие: Среди параллельных осей та проходит через центр масс, для которой момент инерции имеет наименьшее значение.

Аналогичное утверждение справедливо для плоскостей (моментов P).

Пример 2.

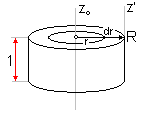
Рассмотрим однородный цилиндр массы M, радиуса R и высотой, равной 1. Записав момент инерции цилиндрического слоя радиуса r и толщиной dr относительно оси z₀ и проинтегрировав от 0 до R получим: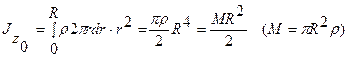

по теореме Штейнера момент инерции цилиндра относительно оси z’ равен

Пример 3.

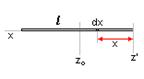
Поместим начало оси x, направленной влево, в правом конце стержня массы M и длины l. Записав момент инерции произвольного элемента dx, находящегося на расстоянии x от оси z’ (лежит в плоскости рисунка) и проинтегрировав по длине стержня получим:

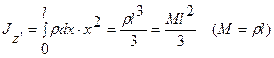
по теореме Штейнера момент инерции цилиндра относительно оси z₀ равен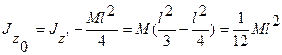

Пример 4. Определим момент инерции однородного эллипсоида с полуосями a,b,c относительно оси x, проходящей через центр эллипсоида. Эту задачу сведем к решенной ранее в этом параграфе задаче о моментах инерции однородного шара, используя тот факт, что преобразование x=ax’,

y=by’, z=cz’ преобразует эллипсоид 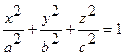в шар единичного радиуса.