Построение теоретического закона распределения признака

 

Для построения теоретического распределения и проверки согласия по критерию хи-квадрат Пирсона надо далее заполнить (дополнить двумя столбцами) таблицу, уже полученную в Excel в результате применения процедуры Гистограмма (рис. 14).

 

 

Границы интервалов

группировки

 

Эмпирические Теоретические

частоты частоты

 

 

Статистика критерия

Пирсона

Рис. 14. Таблица для построения теоретического распределения частоты .

 

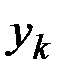– границы интервалов группировки (карманы)

 

– эмпирическая (наблюденная) частота, количество элементов выборки, попавших в i–ый интервал (частота – получена в результате процедуры Гистограмма);

 

 

Эта таблица в Excel (рис. 14.) аналогично той, что была дана в лекции (таблица 1)

 

Таблица №1

 

границы интервалов группировки карманы	эмпирическая частота	теоретическая частота	статистика
…	…	…	…

 

 

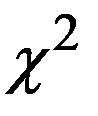
– теоретическая (ожидаемая) частота попадания элементов выборки в i-ый интервал группировки для принятой гипотезы о нормальном распределении генеральной совокупности.

 

В четвертом столбце вычисляется статистика хи-квадрат Пирсона

 

Теоретическая частота попадания признака в интервал определяется по формуле

 

.

Или ,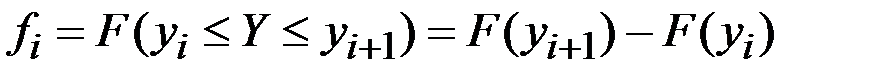

 

где накопленная частота – сумма частот признака, попавшего в промежуток

 

 

 

– теоретическая (ожидаемая) частота попадания элементов выборки в i–ый интервал группировки для принятой гипотезе о нормальном распределении генеральной совокупности в Excel вычисляется с использованием функцией НОРМРАСП.

Для вычисления необходимо вызвать Мастер функций → Статистические → НОРМРАСП и заполнить поля ввода, как показано на рис. 15.

 

 

Рис. 15. Диалоговое окно НОРМОАСП с заполненными полями ввода.

 

В поле x – внесите адрес ячейки верхней границы первого кармана, первого интервала группировки (y₁ = 98)

В поляСреднее; Стандартное_откл – адреса соответствующих ячеек таблицы описательной статистики;

В поле Интегральнаявнесите1(что означает вычисление накопленных частот)

 

В строке формул появится запись

Это выражение в строке формул умножьте на объем выборки N = 53

 

 

В выделенную ячейку, таким образом, как показано на рис. 15, будет внесена формула

= (НОРМРАСП(y₁; среднее; стандартное_откл; 1)* N для

вычисления теоретической частоты попадания признака в интервал .

 

 

НОРМРАСП(A70;E23;E27;1)

 

Рис. 16. Таблица для построения теоретического распределения частоты .

 

В ячейке появится теоретическое значение числа попаданий признак в промежуток (может быть и дробное).

 

 

 

Рис. 17. Таблица с вычисленным значением = НОРМРАСП(A70;$E$23;$E$27;1).

 

 

В следующую ячейку внесите формулу, используя процедуру НОРМРАСП.

= (НОРМРАСП(y_i; среднее; стандартное_откл; 1) –

– НОРМРАСП(y_i-1; среднее; стандартное_откл; 1))* N.

 

В строке формул эта запись будет иметь следующий вид

 

 

Размножьте эту формулу в остальные ячейки столбца соответствующие всем оставшимся карманам (рис. 17).

 

 

 

Рис. 17. Таблица с вычисленными значениями теоретических частот

= (НОРМРАСП(A71; $E$23; $E$27; 1) – НОРМРАСП(A70; $E$23; $E$27; 1))* 53.

 

В выделенную курсором ячейку (рис. 17.) внесите формулу для вычисления частоты попадания признака в промежуток .

=(1 – НОРМРАСП(y_k; среднее; стандартное_откл; 1))*N

 

y_k – верхняя граница последнего кармана

 

В строке формул появится запись

 

Окончательный вид таблицы с полностью заполненным результатами вычислений столбцом показан на рис. 18.

В нижней ячейке столбца вычислена сумма теоретических частот которая должна равняться объему выборки N = 53

 

 

Рис. 18. Таблица значений теоретических частот нормального распределения,

столбец

 

Теперь можно построить совместный график гистограммы частот и теоретического нормального распределения.

 

Щелкните правой кнопкой мыши по любому столбцу гистограммы →в открывшемся окне → Выбрать данные… в диалоговом окне Выбор источника данных выбрать Добавить →заполнить поля ввода диалогового окнаИзменения ряда:

Имя ряда: - ,

Значения: массив (столбец) значений теоретических частот

 

 

Рис. 19. Совмещенный график гистограммы эмпирических и теоретических частот

 

 

Измените тип диаграммы, для этого щелкните правой кнопкой мыши по одному из появившихся столбцов графика → Изменить тип диаграммы ряда… → Точечная →выберите гладкую линию. OK

 

 

 

 

Рис. 20. Совмещенный график гистограммы и теоретического нормального распределения