Проверить значимость коэффициента парной регрессии.

На основании таблицы вычислить линейный коэффициент парной корреляции.

= =0,1488

 

Вывод: Так как линейный коэффициент парной корреляции =0,1488,

отсюда следует, что между признаками X и Y наблюдается слабая прямая линейная зависимость.

 

 

Проверить значимость коэффициента парной регрессии.

Для оценки статистической значимости линейного коэффициента парной корреляции применяется t-критерий Стьюдента. Согласно t-критерию выдвигается гипотеза о случайной природе показателей, т. е. о незначимом их отличии от нуля. Далее рассчитываются фактические значения критерия для оцениваемого коэффициента корреляции путем сопоставления их значений с величиной стандартной ошибки:

 

=

 

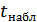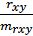
Стандартная ошибка коэффициента корреляции определяются по формуле:

 

1. =

 

= =0,1526

 

2. 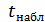= =0,9751

 

(0,05;42)=2,0180

 

Вывод: Фактическое значение сравниваем с табличным критическим значением:

t_набл > t_крит , то не отклоняется, то есть признаётся случайная природа формирования . Коэффициент признаётся незначимым.