Физические основы инфракрасных приборов

 

Закон Планка получен на основании квантовых представлений об излучениях и характеризует спектральное распределение мощности излучения идеального излучателя для малого интервала длин волн Dl в зависимости от термодинамической температуры Т и длины волны l. Спектральная плотность (интенсивность) энергетической светимости идеального излучателя в пределах полусферы в интервале длин волн от l до l+Dl при термодинамической температуре Т определяется формулой Планка:

, (4.1)

 

где r_l,T - спектральная интенсивность плотности излучения абсолютно черного тела при температуре Т; l - длина волны в см; с₁ и с₂ - постоянные излучения c₁= =3.74010^-12Втсм², с₂=1.439 смград.

Примеры зависимостей r_l,Т(l,Т) приведены на рис. 4.1.

 

r_l,Т

0,1

				Т= 600
					Т=500
0,05
						Т=400
								Т=300

4 8 12 16 20 l, мкм

 

Рис. 4.1

 

Закон Стефана - Больцмана. Для получения суммарной энергетической светимости излучения идеального излучателя (абсолютно черного тела ) при данной термодинамической температуре проинтегрируем правую часть формулы Планка (4.1) по длине волны на всем интервале l от 0 до :

,

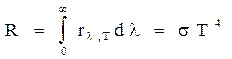где R - плотность излучения абсолютно черного тела при темпера-туре Т, Вт/см²; s=5.670*10^-12Вт/(смград) - постоянная Стефана - Больцмана. Для реальных тел

 

, (4.3)

где e - коэффициент излучения, характеризующий отличие излучательных свойств реального тела от идеального излучателя e < 1.

Закон Вина (закон смещения). Зависимость длины волны l_m, соответствующей максимуму энергии в излучении идеального излучателя, обратно пропорциональна его термодинамической температуре:

,

 

где l_m - длина волны, соответствующая максимальному значению спектральной интенсивности абсолютно черного тела (мкм), с=2898 мкмград - постоянная закона смещения.

Закон Ламберта. Этот закон характеризует излучательную способность поверхности тела и записывается в виде

 

dФ_w = dФ_н соsa dw, (4.4)

 

где dФ_w - лучистый поток, излучаемый малым элементом поверхности в малом телесном угле в направлении, образующем с нормалью угол a; dФ_н лучистый поток, излучаемый малым элементом поверхности по нормали. Закон Ламберта называют законом косинуса (рис. 4.2).

 

a

dФ_н

dФ_w

 

 

Рис. 4. 2

Сила излучения I представляет собой отношение лучистого пото-ка Ф, излучаемого внутри телесного угла w к величине этого угла. Поэтому закон Ламберта иногда записывают в виде

 

, (4.5)

 

где I_н - сила излучения в направлении, перпендикулярном поверхности. Распределение силы излучения соответствует рис. 4. 2. Кривая распределения представляет окружность, касающуюся излучающей поверхности. Отметим, что закон Ламберта выполняется строго только для абсолютно черного тела и идеально рассеивающих или идеально матовых поверхностей.