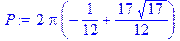Выявление точек разрыва (в том числе у кусочно-заданной функции).
Лабораторная работа №4
1. Вычислить:
1.1. предел функции  ,
,  ;
;
> Limit((2*x*sin(x))/(1-cos(x)),x=0)=limit((2*x*sin(x))/(1-cos(x)),x=0);

> Limit((2*x^2-x-1)/(x^3+2*x^2-x-2),x=1)=limit((2*x^2-x-1)/(x^3+2*x^2-x-2),x=1);

1.2. односторонние пределы функции 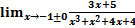
> Limit((3*x+5)/(x^3+x^2+4*x+4),x=-1+0,left)=limit((3*x+5)/(x^3+x^2+4*x+4),x=-1+0,left);

> Limit((3*x+5)/(x^3+x^2+4*x+4),x=-1+0,right)=limit((3*x+5)/(x^3+x^2+4*x+4),x=-1+0,right);
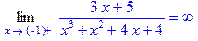
Выявление точек разрыва (в том числе у кусочно-заданной функции).
1) Задаем функцию  и проверяем на непрерывность
и проверяем на непрерывность
> f:=(x^2-x)/abs(x-1);

> iscont(f,x=-infinity..+infinity);

Значение false показывает, что существуют точки разрыва
> discont(f,x);

2) Теперь выявим точки разрыва у кусочно-заданной функции 
> f1:=piecewise(x<-2,2/(x+2),x>=-2 and x<=2,2,x>2, 1/(2*x));
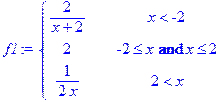
Исследуем на непрерывность точку 
> limit(f1,x=-2,left);

> limit(f1,x=-2,right);
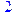
Левосторонний предел бесконечен, значит, функция терпит разрыв 2-го рода в точке  .
.
Исследуем на непрерывность точку 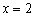
> limit(f1,x=2,left);
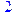
> limit(f1,x=2,right);

Односторонние пределы конечны и различны, значит, функция  терпит разрыв 1-го рода в точке
терпит разрыв 1-го рода в точке 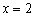 .
.
3. Решение задачи о нахождении производной функции (y',y'') + упрощение выражения.
> g:=(sin(x/3))^2;
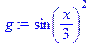
Ищем ее первую и вторую производную
> g1:=diff(g,x);
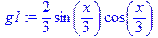
> g2:=diff(g1,x);

или
> diff(g, x$2);
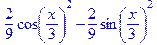
Упрощаем выражение
> simplify(g2);

4. Найти максимальное и минимальное значения функции 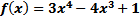 на отрезке [0,3].
на отрезке [0,3].
> f:=3*x^4-4*x^3+1;
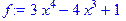
> maximize(f,x,x=0..3,location);

> minimize(f,x,x=0..3,location);
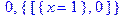
> plot(3*x^4-4*x^3+1, x=0..3);
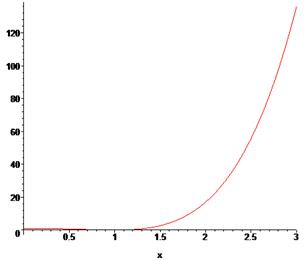
5. Полное исследование функции  (асимптоты, экстремумы, точки перегиба) и построение графика с асимптотами.
(асимптоты, экстремумы, точки перегиба) и построение графика с асимптотами.
Вертикальные асимптоты:
> solve(x^2-2*x=0);
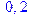
Горизонтальные асимптоты:
> limit(f,x=infinity);
Наклонные асимптоты:
> k:=limit(f/x, x=+infinity);

ð Наклонных асимптот нет
Точки экстремума:
> extrema(f, {},x,'s');
ð Точек экстремума нет
Точки перегиба:
> d:=diff(f,x$2):
> solve(d<0);

> solve(d>0);

Точками перегиба могут служить точки 0, 1, 2.
> simplify(d);

Однако очевидно, что вторая производная в точках 0 и 2 не существует => точка перегиба:1.
> plot(f,x=-10..5, y=-10..10, colour=blue);

6. Геометрические приложения определенного интеграла.
6.1.Вычислить площадь фигуры, ограниченной линиями 

 .
.
> y1:=x+2;
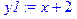
> y2:=2*x-(x^2)/2+6;
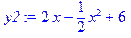
> solve(y1=y2,x);

> with(plots):
> p1:=plot(y1, x=-3..5, y=0..10):
> p2:=plot(y2,x=-3..5, y=0..10):
> display(p1,p2);

> Int(y2-y1, x=-2..4)=int(y2-y1, x=-2..4);
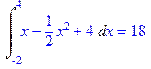
6.2.Вычислить длину дуги кривой, заданную в полярной системе координат ,
, 
> r:=3*(1+sin(x));
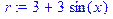
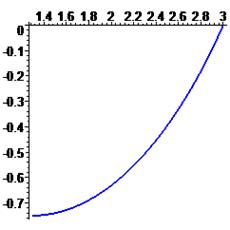
> plot(r,x=-Pi/6..0, coords=polar, colour=blue, thickness=2);
> r1:=diff(r,x);

> Int(r^2+r1^2, x=-Pi/6..0)=int(r^2+r1^2, x=-Pi/6..0);

6.3.Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями  ,
,  ,
,  и
и 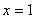 .
.
> y1:=2*x+1;

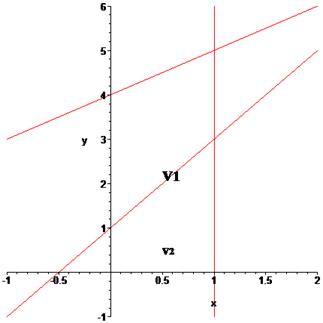
> y2:=x+4;
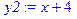
> p1:=plot(y1,x=-1..2, y=-1..6):
> p2:=plot(y2,x=-1..2, y=-1..6):
> p3:=plots[implicitplot](x=0,x=-1..2, y=-1..6):
> p4:=plots[implicitplot](x=1,x=-1..2, y=-1..6):
> p5:=textplot([0.5,2.2,"V1"],font=[TIMES, BOLD, 15], align=RIGHT):
> p6:=textplot([0.5,0.5,"V2"],font=[TIMES, BOLD, 10], align=RIGHT):
> display(p1,p2,p3,p4,p5,p6);
> V:=Pi*int((x+4)^2, x=0..1)-Pi*int(((2*x+1)^2),x=0..1);

6.4.Вычислить площадь поверхности тела, полученного вращением параболы 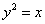 вокруг оси
вокруг оси  на промежутке
на промежутке 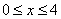 .
.
Вычислим площадь поверхности, образованной вращением верхней ветви 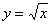 вокруг оси абсцисс. Используем формулу
вокруг оси абсцисс. Используем формулу 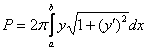
> y:=sqrt(x);

> y1:=diff(y,x);

> P:=2*Pi*int(y*sqrt(1+y1^2),x=0..4);