Понятие о выпуклом программировании

Рис. 3.5

Тогда

C_хр = a С_м q₀ /2. (3.3)

Подставим в (3.1) уравнения (3.2) и (3.3), получим общие минимизи-рующие затраты, связанные с дисциплиной доставки и хранения:

F = C_г + C_хр = + a С_м min. (3.4)

Найдем зависимость F(q₀ ), где переменной является размер одной поставки.

График этой функции покажем на рис. 3.3.

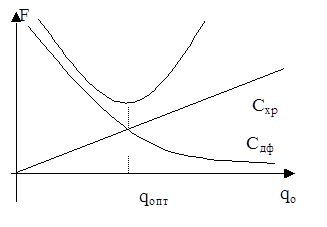
Рис. 3.3.

Полагая, что F(q₀ ) - непрерывная функция, найдем ее минимум путем приравнивания первой производной к нулю:

.

Из этого выражения найдем

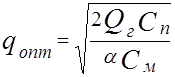. (3.5)

Выражение (3.5) известно под названием формулы Миттенена, которая определяет размер партии, экономической величины заказа, т.е. q_опт.

Найдем время между двумя поставками:

 

.

 

 

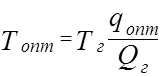Подставим в него уравнение (3.5):

 

 

,

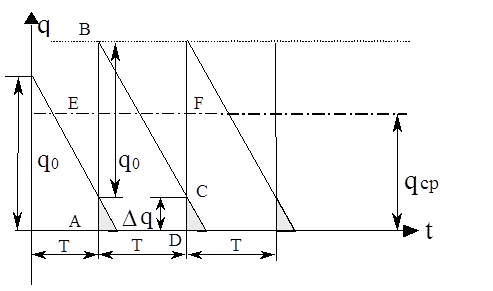где Т_г - длительность года в соответствующих единицах.

Рис. 3.4.

В реальных условиях пополнение запасов производится в течение некоторого времени или с опережением, или с запаздыванием, а также неравномерно и стохастически (случайно). В результате может получиться дефицит материала, поэтому следующий заказ подают раньше, чем израсходован материал.

В связи с этим поставки начинаются тогда, когда на складе могут остаться материалы Dq. Поскольку материалы расходуются неравномерно, из площади трапеции ABCD (рис. 3.4) находим :

q_ср = q₀ /2 + Dq.

Подставим это значение в (3.2):

F = + a С_м (q) ® min.

Полагая, что Dq = const, найдем из полученного выражения размер оптимальной поставки:

F'(q₀ ) = 0.

Имеем

.

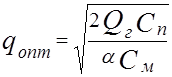Полученные результаты показывают, что величина постоянного переходного запаса увеличивает затраты на содержание складского хозяйства, но не влияет на размер заказа.

Величина переходного запаса может быть обоснована путем сравнения затрат на содержание дополнительного запаса и возможных потерь в связи с простоями производства и с отсутствием материала.

 

3.3. Определение оптимальной частоты обращения

пригородных поездов

Необходимо найти оптимальную частоту обращения пригородных поездов на участке в час “пик”. При этом ставится задача свести к минимуму суммы, зависящие от числа поездов, издержек транспорта и потерь времени пассажирами, приведенных в денежное выражение с помощью условной оценки - человеко-час ожидания. Положим, длина участка равна L = 25 км, расходы на поездо-километр равны RP = 1,5 руб.; ожидаемый пассажиропоток в час “пик” в каждую сторону Г= 4000 чел./ч; оценка пассажиро-часа ожидания RO= 20 коп. Вместимость поезда - 2000 чел.; пропускная способность для пригородных поездов - 5 пар/ч.

Обозначим через X число пар пригородных поездов в час. Тогда получаем следующие ограничения:

1) X £ 5 - по пропускной способности;

2) X ³ 4000/2000=2 - исходя из величины потока и вместимости поезда.

Полагаем, что пассажиры прибывают на станцию посадки равномерно в течение всего интервала между поездами, тогда среднее время ожидания поезда каждым пассажиром составит половину интервала

t = 1/(2X),

а общая затрата пассажиро-ч за 1 ч будет

2Г·t = Г/ X.

сумма расходов в час составит

F= 2L·X·RP + Г·RO /X.

Здесь первый член равен расходам железной дороги, связанной с поездо-км, второй представляет оценку времени ожидания.

Целевая функция зависит лишь от одной переменной и является нелинейной (X^-1).

Для определения оптимального числа поездов продифференцируем F по X и приравняем производную нулю.

= 0;

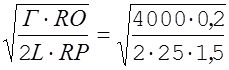X==3,25

Дробное значение X в данном случае допустимо. X = 3,25 означает, что рациональный интервал между поездами равен 60 : 3,25 = 18 мин. Наличие при значении X= 3,25 минимума, а не максимума можно проверить, взяв вторую производную

.

Поскольку X лежит в допустимом интервале (2 £ X £ 5 ) , то принимаем его за оптимальное - X_опт = 3,25.

Если бы X_опт вышло за пределы интервала (X = 6 ), то следует принять для практического использования ближайшее допустимое значение (X = 5 ).

Рассмотрим более сложный случай, когда необходимо оптимизировать несколько переменных, связанных общими ограничениями. Пусть, например, нужно назначить оптимальные размеры пригородного движения не в одном, а в двух направлениях железнодорожного узла. Данные по первому направлению те же, что приведены ранее. Во втором направлении L₂ = 30 км, R⁽²⁾p =1,3 руб.; пассажиропоток в час “пик” - 8000 чел./ч в каждую сторону; свободная пропускная способность - 8 пар поездов/ч; остальные данные такие же, как и для первого участка. Оптимальные размеры движения на втором участке определим прежним способом:

X₂ = 4,5поезда/ч,

т.е. оптимальный интервал обращения поездов равен 60 : 4,5 = 13 мин.

Однако реальные размеры движения ограничиваются не только пропускной способностью каждого участка, но и общим парком электросекций для обслуживания всех вместе взятых пригородных зон узла.

Потребный парк составов для каждого участка (рабочий парк) N_P можно определить по формуле

N_P = A·X ,

где A - оборот состава в часах; X - число поездов в час.

При наличии двух участков имеем

N_P = A₁ X₁ + A₂ X₂ .

Если оборот состава на первом и втором участках равен соответственно 2 и 2,5 ч, а общее число составов, имеющихся в распоряжении, 16, то получим следующие ограничения числа поездов в час по участкам:

x₁5,

(3.6)

x₂8,

2x₁ + 2,5x₂ 16,

x₁5,

x₂8.

Первые два неравенства представляют собой ограничение пропускной способности соответственно на первом и втором участках; третье - ограничение числа используемых составов; четвертое и пятое неравенства устанавливают минимально допустимое число поездов на каждом участке. Сумма расходов по обеим направлениям составит

F = 2L₁·Rp¹ ·X₁ + Г₁·Ro¹ /X₁ + 2L₂·Rp² ·X₂ + Г₂·Ro² /X₂ =

= 75X₁ + 78X₂ + 800/X₁ + 1600/X₂. (3.7)

Задача определения оптимальных размеров движения сводится к минимизации функции F с учетом ограничений (3.6).

Анализ ограничений (3.6) показывает, что второе неравенство лишнее, т.к. даже если X₁ = 0, третье неравенство удовлетворяется только при X₂ £ 16/ 2,5 = 6,4. Следовательно, пропускная способность второго участка не будет полностью использована даже при сосредоточении на нем всех имеющихся составов, и второе из неравенств (3.6) далее не учитываем. Поскольку в рассматриваемой задаче две переменных, то её легко представить геометрически.

Откладываем X₁ и X₂ по двум осям, а значение суммы расходов F - по воображаемой оси, перпендикулярной плоскости чертежа (рис. 3.5). Допустимое сочетание лежит внутри затемненной фигуры ABC. Расходы по каждому варианту соответствуют точке пространства на расстоянии F над точкой (X₁ , X₂ ). Если значения переменных X₁ и X₂ изменяются непрерывно (могут быть дробными), то функция цели F изображается криволинейной поверхностью в пространстве.

 

Возможность точного решения зависит от того является ли целевая функция выпуклой.

Напомним понятия выпуклой функции на примере функции одной переменной, изображенной на плоскости (рис. 3.6).

Функция выпукла, если прямолинейный отрезок, соединяющий любые две точки кривой, полностью лежит выше самой кривой. Если любой такой отрезок лежит ниже кривой, то функция вогнута.

Рис. 3.6

Аналогично можно представить выпуклые и вогнутые функции в пространстве: так, сферический купол здания изображает вогнутую функцию, а сферическое дно резервуара - выпуклую. Для функций более двух переменных геометрическая наглядность теряется, но сохраняется аналитическое определение свойства выпуклости. Функция F(X) выпукла, если для двух любых точек X₁ и X₂ при любом

0m1

справедливо неравенство

F(mX₁ + (1- m)X₂) mF(X₁) + (1- m)F(X₂)

где X - совокупность значений ряда переменных, определяющих функцию (например, конкретное число поездов на первом, втором, третьем участке).

На рис. 3.5 функции 1, 2, 3 - выпуклые, а 4, 5, 6, 7 - вогнутые, функция 8 не относится ни к одному из этих видов. Функция 9 имеет разрыв, поэтому так же не относится ни к одному из видов. Из сравнения 3 и 7 видно, что если F(X) выпукла, то -F(X) вогнута, и наоборот. Выпуклые функции имеют не более одного минимума, вогнутые - не более одного максимума. Функция 8 может иметь много минимумов и много максимумов (так, кривая 8 имеет минимумы при X=A и X= B). В этом случае минимум с наименьшим значением F(X) называют глобальным (общим), а остальные - локальные (местные). Та же терминология применяется и к максимумам, если их несколько.

Задачи оптимизации с нелинейными целевыми функциями могут быть точно решены при двух условиях:

1. Допустимое значение переменных X_i образуют выпуклую область. На нашем рисунке затемненная область возможных решений выпукла.

2. Целевая функция, сводимая к минимуму, должна быть выпуклой (1-3), а к максимуму - вогнутой.

Этими методами решаются задачи на минимум расходов, если расходы - выпуклая функция, и на максимум продукции или прибыли, если это вогнутые функции.

При анализе конкретной задачи необходимо определить характер целевой функции. Задача упрощается, если целевая функция - это сумма слагаемых, каждое из которых зависит лишь от одной переменной:

F(x₁,…,x_n) = F(x₁) + … + F_n(x_n).