Интерполяционный многочлен Ньютона

Интерполирование по формуле Лагранжа имеет недостаток: в этой формуле каждое из слагаемых представляет многочлен n-й степени и при увеличении числа точек x_i и соответственно степени многочлена вычисления по формуле Лагранжа надо производить заново, так как каждое слагаемое формулы зависит от всех точек. От указанного недостатка свободен интерполяционный многочлен Ньютона. Введем предварительно понятие разделенных разностей.

Разделенные разности первого порядка

.

Разделенные разности второго порядка

.

Разделенные разности n-го порядка

.

Здесь i = 0, n-1.

С учетом обозначений интерполяционный многочлен Ньютона имеет вид

P_n (x) = f(x₀ ) + (x - x₀ )f(x₀ , x₁ ) + (x - x₀ ) (x –x₁ )f(x₀ , x₁ , x₂ ) + …

+ (x - x₀ ) (x –x₁ ) … (x –x_n-1 ) f(x₀ , x₁ , … , x_n ).

Погрешность интерполяции можно определить по формуле

R(x) = 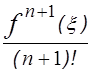(x - x₀ ) (x –x₁ ) … (x –x_n ),

где .

В силу того, что любой i- й член полинома Ньютона зависит только от первых i точек x_i и от значений функций в них, добавление новых точек вызывает лишь добавление новых слагаемых без изменения первоначальных. Это является существенным преимуществом данного многочлена по сравнению с многочленом Лагранжа. При n = 1 из формулы многочлена Ньютона получим линейную интерполяцию

P₁ (x) = f( x₀ ) + (x – x₀ )(f(x₁ ) – f(x₀ ))/(x₁ - x₀ ).