Точность вычислительного эксперимента

Таблица 2

Рис. 4

Параметр c_ij определяет значение коэффициентов целевой функции,

αij - нормы расхода ресурсов на единицу продукции, b_i - распола­гаемые ресурсы. Все эти величины, особенно aij , bi, зависят от целого ряда случайных факторов (исправности оборудования, своевре­менности поставки ресурсов и т.д.) и поэтому являются случайными величинами, что необходимо учитывать в ходе исследований.

Переменные могут быть непрерывными и дискретными. Непрерывными называются величины, которые в заданном интервале могут принимать любые значения (выпуск хлеба, тканей и т.д.).

Дискретными или целочисленными считают такие величины, которые могут принимать только целые значения. Например, нельзя подать под поезд 0,43 тепловоза. Частным случаем целочисленных переменных являются булевы переменные. Они названы по имени английского математика Дж. Буля. Булевы переменные могут принимать только значения 0 илиI, где I означает “истина”, “да”, a 0- ложь”, “нет”. Эти переменные могут быть использованы при решении задач о назначениях.

Зависимости между переменными быть линейными и нелинейными. Напомним, что линей2ными называют такие зависимости, в которых переменные входят в первой степени. Если же переменные входят не в первой степени или есть произведения переменных, то зависимости нелинейными. Сочетания различных элементов модели приводят к различным задачам. Так, задачи. Содержащие детерминированные параметры. Непрерывные переменные и линейные зависимости - это задачи линейного программирования. Если переменные целочисленные, то задачи относятся к классу целочисленного программирования, при параметрах случайных - к задачам стохастического программирования, при зависимостях нелинейных - к задачам нелинейного программирования.

Все возможные сочетания элементов моделей составляют класс задач математического программирования. Таким образом, в общем случае задачи принятия решения применительно к математической модели представляют собой задачи математического программирования.

Наиболее распространенным типом задач математического программирования являются задачи ЛП, с помощью которых решается большой класс задач принятия решений, в том числе задачи оптимального планирования. Задачи целочисленного и нелинейного программирования решаются сведением их к задачам ЛП. Задачи стохастического программирования сводятся к нелинейным, которые, в свою очередь, для решения представляются в форме задач ЛП.

I.6. Методы и модели оптимизации

Количество внутренних состояний сложных кибернетических систем, включающих в свой состав ряд локальных объектов и процессов, может быть очень большим. Анализ таких систем представляет собой трудную и громоздкую по вычислениям задачу. Решение которой требует больших затрат труда и времени. Внешние факторы воздействующие на систему, еще более разнообразят и усложняют ее функционирование. Наличие неустойчивых и нерегулярных связей вносит в динамическое поведение системы элементы неопределенности и случайности.

В дальнейшем под термином анализ системы понимается метод исследования сферы организационного управления.

При управлении перевозочным процессом на железнодорожном транспорте часто необходимо принимать решения в ситуациях, определяемых сотнями, а иногда и тысячами факторов и взаимных связей. Принятия неоптимальных решений в таких условиях приводит к нерациональному использованию ресурсов, несогласованности в работе звеньев железнодорожного конвейера. В связи с этим сфера организационного управления стала предметом изучения ряда научных дисциплин. Среди естественных и технических наук наиболее важное место принадлежит кибернетике. Кибернетику определяют как науку, изучающую общие закономерности строения сложных систем управления и протекания в них процессов управления. А так как любые процессы управления связаны с принятием решения на основе получаемой информации, то кибернетику определяют еще и как науку об общих законах получения, хранения, передачи и преобразования информации в сложных управляющих системах. Однако кибернетика является общетехнической базой исследования, прикладным же направлением кибернетики, непосредственно решающим практические организационные задачи, служит научная дисциплина, называемая исследованием операций (ИСО).

Методы ИСО предназначены для выработки объективных количественных рекомендаций по управлению целенаправленными процессами. Принятие решений при этом имеет три основные части:

1) цели;

2) пути достижения выбранных целей;

3) способы распределения ограниченных ресурсов.

Основная цель ИСО – объективно разобраться в каждой задачи, предлагаемой лицами, ответственными за принятие решений, и численно оценить различные варианты достижения цели. Таким образом, ИСО – это прикладная наука, занимающаяся количественным обоснованием

принимаемых решений, связанных с оптимальным управлением органи­зационными системами.

1.7. Основные понятия исследования операции

Операция. Эффективность операции. Под операцией бу­дем понимать любое мероприятие (или систему действий), объединен­ное единым замыслом и направленное на достижение цели. Операция является управляемым мероприятием, т.е. от нас зави­сит, выбрать тем или другим способом какие-то параметры, характе­ризующие способ ее организации. Всякий определенный выбор завися­щих от нас параметров мы будем называть решением. Решения могут быть удачными и неудачными, разумными и неразумными. Оп­тимальными называются решения, которые по тем или иным соображениям предпочтительнее других. Основная задача исследования операций - предварительное количественное обо­снование оптимальных решений.

Рассмотрим отдельную операцию. Размышляя над организацией опера­ции, мы стремимся сделать ее более эффективной. Под эффек­тивность» операции подразумевается степень ее приспособ­ленности к выполнению, стоящей перед ней задачи. Чем лучше органи­зована операция, тем она эффективнее.

Чтобы судить об эффективности и сравнивать между собой по этому параметру различно организованные операции, нужно иметь некоторый числовой критерий оценки, или показатель эффективности (целевая функция), отражающий цель операции в количественной форме.

Целевая функция является математическим выражением результата действия процесса. Ее также называют критериальной функцией, крите­рием эффективности или показателем качества. Выбор целевой функции и нахождение экстремума являются сутью проблемы оптимизации. В от­личие от моделей физических процессов целевые функции обычно выра­жают нефизические величины: прибыль, стоимость качество и т.д.

Основные принципы определения целевых функций выведены на осно­вании опыта [ΙΙ].

1. Принцип однозначности состоит в том, что долж­на максимизироваться или минимизироваться одна целевая функция, т.е. она должна отражать основную, а не второстепенную цель опера­ции.

2. Принцип соответствия заключается в том, что целевая функция должна определяться таким образом, чтобы ее оптимиза­ция обеспечивала наиболее успешное управление процессом.

3. Принцип управляемости состоит в том, что целе­вая функция должна быть выражена через переменные управления.

4. Принцип ориентации на прибыль состоит в том, что целевые функции обычно должны выражать прибыль или ве­личины, которые тесно с ней связаны, например, стоимость и качест­во.

5. Принцип подходящей формы состоит в, исполь­зовании целевой функции, имеющей экстремум. Целевым функциям, не имеющим экстремума, требуется ограничение для обеспечения решения, которое имело бы смысл, например, линейное программирование. Процесс оптимизации должен сводиться к решению уравнений, которые можно использовать для нахождения переменных управления, оптимизирую­щих целевую функцию. Уравнения, которые выражают переменные опти­мального управления через требуемые параметры процесса, называются уравнениями оптимального управле­ния.

Кратко рассмотрим наиболее распространенные виды целевой функ­ции.

Целевая функция стоимости выражает стоимость, связанную с осу­ществлением процесса. Обычно в целевую функцию стоимости включают лишь переменные стоимости, которые поддаются управлению, например, стоимость материалов и топлива. Постоянные стоимости, а также про­чие стоимости, неподдающиеся управлению, включать не следует (на­пример, постоянные капиталовложения, накладные расходы и другие косвенные затраты).

Задачи динамической оптимизации имеют целевые функции, являющиеся категориями функций стоимости во времени. Их можно предста­вить в виде

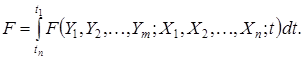
Задача минимизации целевой функции F называется задачей опти­мальной траектории, поскольку конечной целью является выбор такого пути или траектории между двумя граничными условиями, при котором эта функция будет минимизироваться. Она определяет стоимость дости­жения цели управления.

Целевая функция качества. Полезной и удобной формой целевой функции качества является взвешенная квадратная форма. Такая форма определяет оптимальное протекание процесса как состояние, при кото­ром сумма квадратов разностей. Между требуемыми значениями перемен­ных Yj и фактическими их значениями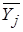минимальна. Переменные состояния могут быть либо измерены, либо вычислены косвенным пу­тем.

Представим целевую функцию качества, присущую установившемуся состоянию:

где y_j – положительные весовые коэффициенты.

Запишем непрерывную динамическую целевую функцию качества в квадратичной форме:

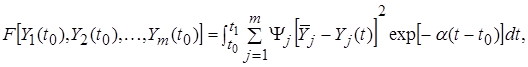
где yj и a - положительные константы, a t₀ - начальное время. Экспоненциальный член является добавочным весовым коэффициентом, зависящим от времени.

Дискретная динамическая целевая функция качества в квадратичной форме имеет вид

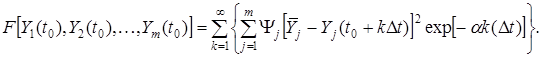
Разница между контролем качества при помощи, динамических целе­вых функций и обычным контролем качества в установившемся состоя­нии заключается в том, что в первом случае стремятся вернуть про­цесс к оптимуму с минимальной стоимостью, тогда как во втором слу­чае динамическая характеристика процесса и скорость достижения но­вой рабочей точки игнорируются.

Целевая функция времени для граничных условий

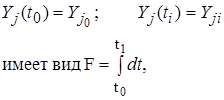
и выражает время протекания процесса между двумя фиксированными граничными условиями.

Целевая функция прибыли может быть определена как разница между общим приходом и затратами. При управлении процессом можно пренеб­речь постоянными затратами, поскольку они входят в целевую функция в качестве постоянного члена и не влияют на положение оптимума. Целевая функция прибыли используется при решении задач методом линейного программирования.

1.8. Неопределенность целей

Задачи, в которых параметры системы определены и любой выбор решения приводит к определенному значению показателя эффективно­сти, мы называем детерминированными.

Гораздо чаще в практике встречаются задачи, когда не все усло­вия известны заранее, а некоторые из них содержат элемент неопре­деленности. Принято различать три типа неопределенности:

1) неопределенность целей;

2) неопределенность наших знаний от внешней среды;

3) неопределенность действий.

Пусть эффективность операций характеризуется по нескольким кри-

териям:

F=f(a₁, a₂, …,a_n; Y₁, Y₂, …, Y_n,; X₁, X₂, …, X_n,).

Здесь Y₁, Y₂, …, Y_n -неизвестные условия или факторы.

Если бы условия Y₁, Y₂, …, Y_n были известны, то заранее мож­но было бы выбрать F и найти такое решение X₁, X₂, …, X_n при котором он может принять экстремальное значение. Но в нашем приме­ре Y₁, Y₂ ,…, Y_n неизвестны, а значит, и F неизвестен при лю­бом решении. Тем не менее задача выбора решения может быть сформу­лирована так:

При заданных условиях a₁, a₂, …,a_n с учетом неизвестных факторов Y₁, Y₂, …, Y_n найти такие, элементы решения X₁, X₂, …, X_n, которые по возможности обращали бы в экс­тремум показатель эффективности F.

Это уже другая, не чисто математическая задача (в формулировке сказано "по возможности"). Наличие неизвестных факторов, Y₁, Y₂, …, Y_n переводит нашу задачу в задачу о выборе решения в условиях неопределенно­сти.

Рассмотрим в качестве примера работу сортировочной станции, стремясь оптимизировать процесс обслуживания прибывающих на эту станцию грузовых поездов. Заранее неизвестны ни точные моменты прибытия поездов, ни адреса, по которым направляются вагоны. Все эти и другие параметры представляют собой случайные величины, за­кон Распределения каждой из которых (и их совокупности) может быть определен по имеющимся данным обычными методами математиче­ской статистики.

В случае, когда Y₁, Y₂, …, Y_n являются случайными величина­ми (или случайными функциями), распределение которых хотя бы ориентировочно известно, для оптимизации решения может быть применен один из двух приемов:

1)искусственное сведение к детерминированной схеме;

2)оптимизация в среднем.

Первый прием сводится к тому, что неопределенная, вероятност­ная картина явлений приближенно заменяется детерминированной. Для этого все случайные факторы приближенно заменяются не случайными (как правило, их математическими ожиданиями). Заметим, что этот прием применяется в тех случаях, когда Y₁, Y₂,…, Y_n обладают большим разбросом, но показатель эффективности F зависит от них линейно (или почти линейно). Второй прием более сложный, применя­ется, когда случайность Y₁, Y₂, …, Y_n весьма существенна и за­мена их математическим ожиданием может привести к большим ошибкам.

Пусть F существенно зависит от Y₁, Y₂, …, Y_n. Положим, что нам известно распределение этих факторов, скажем, плотности распре­деления f (y₁, y₂,…,y_n) пусть операция выполняется много раз, причем Y₁, Y₂,…, Y_n меняются случайным образом. Очевидно, то решение будет наилучшим, при котором операция в среднем будет наиболее эффективна, т.е. математическое ожидание показателя эффективности F будет экстремально.

Таким образом, нужно выбрать такое решение X₁, X₂, …, X_n при котором показатель эффективности принимает экстремум математи­ческого ожидания:

Такую оптимизацию будем называть оптимизацией в среднем. При обос­новании решения в условиях неопределенности следует указывать не одно решение, всегда лучше выделять область приемлемых ре­шений. В пределах этой области можно произвести окончательное при­нятие решения для управления процессом производства.

1.9. Многокритериальные задачи

При решении практических задач эффективность операций приходится оценивать не по одному, а сразу по нескольким показателям - кри­териям эффективности F₁ , F₂ ,…, F_N. Одни из них желательно
сделать больше, другие — меньше. Напомним, что критерий эффективности зависит как от заданных условий (параметров системы), так и от элементов решения:

F=f(a₁, …, a_n; x₁, …x_n). (10)

Если математическая модель построена, будем полагать, что зави­симость (10) нам известна и для "a и "x мы можем найти F. Как правило, эффективность больших по объему сложных операций не может быть полностью охарактеризована с помощью одного показателя. Например, при оценке деятельности предприятия приходится учиты­вать ряд показателей, таких, как прибыль, полный объем продукции, себестоимость и т.д.

Такая множественность F, некоторые из которых нужно максими­зировать, а другие минимизировать, характерна для задач УПП.

Следует подчеркнуть, что приведенные выше требования несовмест­ны. Решение, обращающее в max один из критериев F, как прави­ло, не обращает ни в max ни в min другие критерии Fi. По­этому для научного исследования формулировка "достижение max эф­фекта при min затратах" некорректна. Корректной формулировкой может быть "достижение максимального эффекта при заданных затра­тах" или "достижение заданного эффекта при минимальных затратах".

Ввиду того, что комплексная оценка операции сразу по нескольким параметрам затруднительна, на практике искусственно объединяют не-сколько показателей в один обобщенный показатель (или критерий) F. Нередко в качестве обобщенного критерия берут дробь: в числителе ставят те показатели F₁ F₂ …, F_m, которые желательно увеличить, а в знаменателе - уменьшить:

Общим недостатком составного критерия является то, что недостаток эффективности по одному показателю можно скомпенсировать за счет другого.

Часто составные критерии предлагаются не в виде дроби, а в виде "взвешенной суммы" отдельных показателей эффективности:

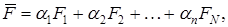
где "a - положительные или отрицательные коэффициенты. Положи­тельные ставятся при тех показателях, которые желательно максими­зировать, отрицательные - минимизировать. Абсолютные значения ко­эффициентов соответствуют степени важности показателей.

Предложенный критерий страдает теми же недостатками, что и при­веденный выше, однако когда "веса" подбираются так, чтобы составной критерий наилучшим образом выполнял свою функцию, удается по­лучить с его помощью некоторые результаты ограниченной ценности.

В некоторых случаях задачу с несколькими критериями удается свести к задаче с одним единственным критерием, если выделить только один, главный, критерий F1 и стремиться обратить его в максимум, а на остальные, вспомогательные критерии F₂ F₃ …, F_n наложить только некоторые ограничения:

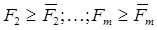
Эти ограничения войдут в комплекс заданных условий.

Рассмотрим следующий пример. При оптимизации плана работы пред­приятия можно потребовать, чтобы прибыль была максимальной, план по ассортименту выполнен, а себестоимость продукции - не выше за­данной.

При такой постановке задачи все критерии, кроме одного, переводят­ся в разряд заданных условий операции. Варианты решения, не укладывающиеся в заданные границы, сразу же отбрасываются, как неконкурентоспособные. Полученные рекомендации будут зависеть от того, как выбраны ограничения для вспомогатель­ных критериев. Чтобы определить, как это влияет на окончательные рекомендации по выбору решения, полезно изменить ограничения в ра­зумных пределах.

Иногда в многокритериальных задачах можно сократить множество
исходных вариантов, т.е. исключить из неформального анализа те варианты решений, о которых заранее известно, что они плохи. Один из подобных путей предложил В.Парето в 1904 году. Изложение принципа В.Парето будем вести по [I3]. Пусть имеется некоторый выбор x* и известно, что существует другой выбор 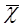, такой, что для всех критериев fi (x) имеет место неравенство

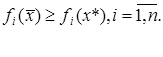
В (11) хотя бы одно из неравенств – строгое. Ясно, что выбор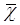
лучше x*. Поэтому все векторы x*, удовлетворяющие (11), можно
исключить из рассмотрения. Далее можно заниматься сопоставлением
только тех векторов x*, для которых не существует 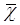такого,
что для всех критериев удовлетворяются неравенства (11). Множество таких значений x* называют множество Парето, а вектор x* называют неулучшаемым вектором р е з у л ь т а т о в (в е к т о р о м П а р е т о). Следова­тельно, если из

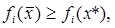
для любого i следует

[13]

Пусть цели системы определяются двумя однозначными функциями

f1(x) ® max, f2(x) ® max,

Тогда каждому допустимому значению переменной x отвечает одна точка на плоскости (f1,f2) , приведенной на рис.5, а равенства f1= f1(x), f2= f2(x) определяют параметрическое задание некото­рой кривой abcd в этой плоскости.

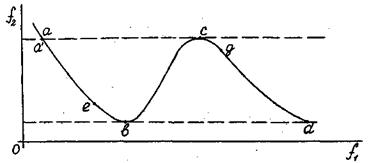
Рис. 5

Но множество Парето это не вся кривая. Например, часть кривой bc не принадлежит, так как вместе с ростом f1 увеличивается и f2.. Значит, на этом участке кривой изменению переменной x отвечает одновременное увеличение обеих целевых функций, поэтому такие ва­рианты решений должны быть сразу исключены из дальнейшего рассмот­рения. Также должен быть исключен из рассмотрения участок a’b, поскольку для каждой его точки в найдется точка, принадлежащая участку cd , в которой значение обеих функций и f1 и f2 больше, чем в точке e . Следовательно, принадлежать к множеству Парето мо­гут только участки aa’ и cd , причем точка a' должна быть исключена.

Принцип Парето заключается в том, чтобы выбирать в качестве ре­шений только тот вектор, который принадлежит множеству Парето. Принцип Парето не выделяет единственного решения, он только сужает множество альтернатив.

Рассмотрим еще один способ построения компромиссного решения, который называется "методом последовательных уступок". Пусть крите­рии расположены в порядке убывающей важности F₁ F₂ …, F_n. Для простоты положим, что каждый из них нужно обратить в максимум. Про­цедура построения компромиссного решения сводится к следующему. Сначала ищется решение, обращающее в максимум главный показатель эффективности (критерий)F₁. Затем, исходя из практических соображений и точности, назначается некоторая "уступка" DF₁, которую мы согласны допустить для того, чтобы обратить в максимум второй критерий F_2. . Налагаем и на показатель F₁ ограничение так, чтобы он был не меньше, чем F*₁ - DF₁ , где F*₁ - максимально возможное значение F₁, при этом ограничении ищем решение, обращающее в мак­симум F₂ . Далее снова назначается "уступка" в критерии DF₂ и т.д.

Такой способ построения компромиссного решения хорош тем, что здесь сразу видно, ценой какой "уступки" в одном критерии приобре­тается выигрыш в другом.

Заметим, что свобода выбора решения, приобретаемая ценой даже незначительных "уступок", может оказаться существенной, так как в районе максимума эффективность решения меняется слабо.

1.10. Выбор целевой функции в условиях неопределенности

Пусть отыскивается наилучшее решение X, при котором максимизиру­ется целевая функция F[10]. На нее оказывают влияние условия Aj проведения операции, значения которых неизвестны. В этом слу­чае необходимо задаться возможными значениями A, т.е. A₁ A₂ …, A_n; возможными значениями X, т.е. X₁ X₂ …, X_n Для всех комбинаций XjAj просчитать целевую функцию Fij. Расчеты удобно представить в виде табл. I.

Используя данные табл. I, обобщим целевую функцию. В дальнейшем целевую функцию будем называть критерием эффективности. Рассмотрим группу критериев, основанных на изве стных вероятностях условий.

Таблица 1.

Xj	A1	A2	…	An
X1	F11	F12	…	F1n
X2	F21	F22	…	F2n
…	…	…	…	…
Xn	Fm1	Fm2	…	Fmn

 

Критерий Лапласа используется, если все условия fii считаются равновероятными, и вы­ражается следующей зависимостью:

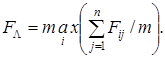(12)

Исходя из этого критерия, определяют оптимальное решение, т.е.

то X_j , при котором имеет место max FÙ. В случае, если известны вероятности P_j, появления условий A_j. , формулу (12) можно запи­сать следующим выражением:

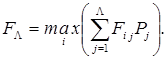(13)

Критерий Вальда называют еще критерием осторожного поведения, максимальным или пессимистическим. По этому критерию оптимальным будет решение, дающее определенный гарантированный выигрыш при наи­худших условиях:

(14)

Применяя критерий Вальда, всегда ориентируются на наихудшие ус­ловия.

Критерий Гурвица, или критерий компромиссного поведения, можно представить следующим выражением:

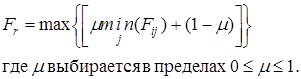(15)

Если m=1, то критерий Гурвица обращается в критерий Вальда; если m= 0, - в критерий "крайнего оптимизма", рекомендующий вы­бирать такое решение, которое приводило бы к наилучшему поведению системы. Значения m выбираются из субъективных соображений: чем опаснее ситуация, тем ближе к единице выбирается значение m.

Критерий Сэвиджа называют еще критерием максимального риска Этот критерий рекомендует в условиях неопределенности выбирать ту стратегию, при которой величина риска принимает наименьшее значение в самой неблагоприятной ситуации, т.е. когда риск максимален. Он имеет вид

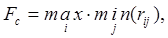(16)

матрица потерь (отрицательная), т.е. величина rij измеряется разностью между фактически полу­ченным результатом и результатом, который можно было бы получить, если были бы известны условия операции.

Сущность этого критерия в том, чтобы любыми путями избежать большого риска при принятии решения.

Пример. Дана матрица с возможными значениями Аj , возможными значениями Xi и значениями Fij, (табл. 2).

 

 

Xi	A1	A2	A3
X1	0,25	0,30	0,15
X2	0,75	0,20	0,35
X3	0,25	0,80	0,25
X4	0,85	0,05	0,45

 

Найти оптимальное решение, используя критерии Вальда, Сэвиджа Гурвица при m = 0,6.

Решение.

1. Критерий Вальда. В каждой строке матрицы вы­берем наименьший выигрыш (табл. 3).

Таблица 3

Xi Aj	A1	A2	A3	Fij
X1	0,25	0,30	0,I5	0,I5
X2	0,75	0,20	0,35	0,20
X3	0,25	0,8	0,25	0,25 *
X4	0,85	0,5	0,45	0,05

 

Из величин F_ij максимальная (отмечена звездочкой) равна 0,25, таким образом, по критерию Вальда, оптимальной является стратегия X₃

2.Критерий Сэвиджа. В исходной матрице строим добавочный столбец и помещаем в нем значения максимального риска в каждой строке (табл. 4).

Таблица 4

Xi Aj	A1	A2	A3	rij
X1	0,65	0,50	0,30	0,65
X2	0,10	0,60	0,10	0,60*
X3	0,60		0,20	0,60*
X4		0,75		0,75

 

Минимальным из значений r_ij является 0,60 (отмечено звездочкой); следовательно, по критерию Сэвиджа оптимальной является любая из стратегий X₂,X₃.

3. Критерий Гурвица. Запишем в правых трех столбцах табл. 5 "пессимистическую" оценку выигрыша, "оптимистическую" и их среднее значение по формуле

где максимальное значение F (отмечено звездочкой) соответствует стратегии X₃ . Таким образом, по критерию Гурвица с небольшим перевесом в сторону пессимизма (m = 0,6) оптимальной стратегией является Х₃ . Следовательно, все три критерия согласия говорят в пользу стратегии Х₃ , которую мы имеем все основания выбирать.

Таблица 5

Xi Aj	A1	A2	A3	ai	wi	FÙ
X1 X2 X3 X4	0,20 0,75 0,25 0,85	0,30 0,20 0,80 0,05	0,15 0,35 0,25 0,45	0,15 0,20 0,25 0,05	0,30 0,75 0,80 0,85	0,21 0,42 0,47 0,37

 

Рассмотренные случаи не исчерпывают всего многообразия принци­пов выбора критериев эффективности, однако с помощью их комбинаций можно получить и более сложные варианты выбора обобщенного крите­рия.

Выше предполагалось, что критерий эффективности поддается в принципе физическому измерению. Однако в ряде случаев не существу­ет способов количественного измерения цели операции. Тогда прихо­дится пользоваться приемом, называемым ранжированием (ранговым под­ходом). При этом критериям эффективности присваиваются оценки -ранга - по заранее выбранной шкале: двухбалльной, пятибалльной и т.д. Ранговый критерий имеет дискретную область определения. В про­стейшем случае область содержит два определения ("да" - "нет", "плохо" - "хорошо", 0-1). Это может соответствовать, например, достижению или недостижению цели операции.

Ранг - это количественная оценка критерия эффективности, носящая субъективный характер, так как качественному признаку ста­вится в соответствие некоторое число.

Ранговый подход имеет большое распространение при проведении Различных экспертных опросов, например, при оценке победителей в спортивных соревнованиях, сравнении произведений искусства, дегус­тации продуктов питания и т.д.

Как было показано выше, математическая модель представляет собой формальное описание основного содержания задачи. Процесс ее составления, как правило, достаточно труден и требует помимо весь­ма глубокого проникновения в сущность моделируемой проблемы опре­деленных познаний в области математического аппарата. В дальнейшем при численном эксперименте на модели предполагается использовать возможности вычислительной техники, с помощью которой этот анализ будет осуществлен. Общая схема составления математических моделей, скажем задач принятия решений и их реализация на ЭВМ могут со­стоять из следующих этапов.

Первый, начальный этап исследования связан с определением факти­ческой задачи, с ее постановкой, т.е. с формулированием цели на обычном языке. Этот этап включает в себя также оценку возможностей решения, перечня различных, но приемлемых вариантов. Иногда данные для такой оценки не удается получить сразу, тогда сама постановка задачи может стать объектом исследования.

На втором этапе необходимо выделить набор параметров, которые описывают процесс принятия решений. Выбор тех или иных численных значений для параметров набора эквивалентен принятию того или ино­го решения. Параметры эти называют параметрами уп­равления, число их может быть весьма значительным. Иногда для этой цели приходится создавать упрощенную модель ситуации.

Далее, на третьем этапе следует на основании предварительного анализа неопределенностей моделируемого объекта выделить и четко сформулировать цель, ради достижения которой принимается то или иное решение. Как было показано выше, целевую установку процесса принятия решения представляют в виде некоторой функции, зависящей от параметров управления, значения которой дают оценку качества принятому решению, т.е. выбирается критерий эффективности, уста­навливаются меры для сравнительной оценки результатов.

Четвертый этап предусматривает анализ всей имеющейся информа­ции, формирование и уточнение заданных условий и ограничений, уточ­нение альтернатив.

На пятом этапе создается математическая модель системы (ситуа­ции, процесса), проверяется ее пригодность с точки зрения охвата всех ключевых факторов, связей и взаимодействий.

На шестом этапе выбирается (или создается методика расчета), и исходные данные преобразуются в форму, пригодную для вычислений. Обычно на этом этапе разрабатывается алгоритм решения задачи на модели и оцениваются трудности программирования, т.е. завершается вся подготовка к решению задачи.

Седьмой этап - реализация вычислительного алгоритма, означающая решение задачи на модели. Часто этот этап разбивается на отдельные фазы в зависимости от полноты модели (ее приспособленности к полно­му решению), совершенства алгоритма или частных целей исследования.

На восьмом этапе производится анализ результатов. Анализ реше­ния бывает двух видов: формальный (математический), когда проверя­ется соответствие полученного решения построенной математической модели (в случае несоответствия проверяются программа, исходные данные, работа на ЭВМ и т.д.), и содержательный (экономический, технологический и т.п.), когда проверяется соответствие полученно­го решения тому объекту, который моделируется. В результате этого анализа в модель могут быть внесены изменения или уточнения, после чего весь разобранный процесс повторяется. Модель считается пост­роенной и завершенной, если она с достаточной точностью характери­зует деятельность объекта по выбранному критерию. Только после это­го модель может быть использована для расчета.

Сущность девятого, последнего этапа состоит в выборе оптимально­го решения задачи, по результатам которого формулируются обоснован­ные рекомендации.

Приведенный перечень условен, и как всякая классификация не пре­тендует на полноту. Кроме того, в зависимости от типа задачи тот или иной этап может отсутствовать, этапы могут объединяться, иног­да может меняться их последовательность. Заметим, что часто дейст­вия имеют творческое содержание и вряд ли могут быть формализованы. Это означает, что автоматизация принятия решений в больших систе­мах управления на каком-то этапе развития неприемлема.

В настоящем курсе, дающем первоначальное представление о мето­дах составления математических моделей и их оптимизации, реальные объекты, естественно, не рассматриваются (исключение составляет разд. 3), а содержательные формулировки задач есть как бы описа­тельные модели, по которым требуется построить модели математиче­ские. Поэтому каждую математическую формулировку задачи будем рас­сматривать как математическую модель реальной ситуации.

1.11. Пример построения математической модели

В качестве примера рассмотрим составление математической модели планирования загрузки технологического оборудования цеха. В зависимости от конкретных условий, которые находят отражение в формирова­нии математической модели и критерии эффективности плана, эта задача может ставиться и решаться по-разному.

Пусть требуется составить план производства трех видов дета­лей - цилиндра, плиты и втулки.

В данном случае могут быть использованы три группы однородного оборудования токарные, строгальные станки и сварочные аппараты. Возможны также различные способы производства, отличающиеся разными затратами времени того или другого вида оборудования на изготовление деталей. Нормы времени (в часах) для трех возможных способов производства (I, П, Ш) приведены в табл. 6.

Таблица 6

Оборудование	Нормы времени для производства, ч	Суммар­ный фонд рабоче­го вре­мени, ч
	цилиндра	плиты	втулки
	I	II	III	I	II	III	I	II	III
Токарные станки	0,4	0,8	1,2	0,4	0,2	-	0,4	0,2	-
Строгальные станки	0,4	-	0,2	0.6	0,2	0,4	0,2	1,2	1,6
Сварочные аппараты	0,4	0,6	0,2	0,8	1,6	2,0	1,4	0,8	0,4
План

 

В последнем столбце указан суммарный фонд рабочего времени на производстве деталей по каждой группе оборудования, а в последней строке дан план производства по каждому наименованию деталей. Из табл. 6 видно, что при первом способе производства цилиндр обраба­тывается на всех видах оборудования по 0,42 ч; при втором способе эта деталь проходит обработку на токарном станке в течение 0,82 ч и на сварочном - 0,62 ч. Наконец, при третьем способе цилиндр об­рабатывается на всех видах оборудования с нормами времени, указан­ными в третьем столбце.

В задаче планирования искомые неизвестные x₁ - количество де­талей, которое нужно изготовить по тому или иному способу произ­водства для достижения максимального эффекта. Через x₁, x₂, x₃ обо­значено количество цилиндров, изготовленных соответственно первым, вторым и третьим способами; аналогичный смысл имеют обозначения остальных неизвестных.

Запишем теперь три группы ограничений задачи, вытекающих из ус­ловий производства.

I. Ограничения по фондам машинного времени для каждой группы оборудования. При принятых обозначениях эти ограничения имеют сле­дующий вид: (17)

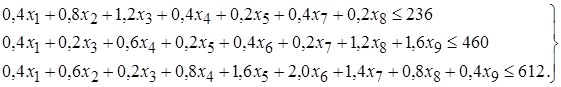
Приведенные неравенства соответствуют условию: затраты времени на производство изделий должны быть равны или меньше фонда времени, выделенного для этой цели по каждой группе оборудования.

II. Ограничения, определенные программой.

(18)

Ш. Ограничение, вытекающее из физического смысла переменных.

Поскольку переменные не могут быть отрицательными величинами, то x_i>=0 ( i= 1,2,...,9). (19)

Наконец, нужно указать критерий оптимальности плана загрузки оборудования. Положим, что в рассматриваемом случае план должен обеспечить максимальную загрузку оборудования. Это означает, что переменные x_i должны быть выбраны так, чтобы суммарные затраты машинного времени по всем трем группам имели максимальные значения (сравнительно с их значениями для любых других вариантов плана). Критерий оптимальности имеет при этом следующее выражение:

(20)

Сформулируем рассматриваемую задачу математически:

- найти неизвестные x_i при ограничениях формул (17-19) та­ким образом, чтобы функция (20), определяющая суммарное использо­вание оборудования, достигла максимального значения.

Формулы (17-19) совместно с функцией (20) являются математи­ческой моделью планирования загрузки оборудования.

В качестве критерия качества плана может быть принят и другой показатель, например, прибыль. Тогда критерием оптимальности пла­на будет максимум прибыли. Могут быть поставлены требования комп­лектности в выпуске деталей (например, один комплект должен со­стоять из одного цилиндра, двух плит и трех втулок), а оптималь­ный план должен обеспечить выпуск максимального количества комп­лектов.

Таким образом, постановки задачи могут быть столь же разнооб­разны, как и цели, и конкретные условия планирования производства. В соответствии с ними будет меняться структура математической мо­дели - ее ограничение, критерий оптимальности и результативные по­казатели оптимального плана.

В модели плана, обеспечивающего максимальную прибыль и не лими­тирующего количество изготовляемых деталей, ограничения (17) и (19) не изменяются, ограничения (18) пропадают, а критерий опти­мальности примет следующий вид:

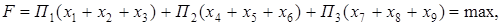(21)

где П₁, П₂, П₃ - прибыль, получаемая на одну деталь: цилиндр, плиту и втулку соответственно.

Построенная модель оптимальной загрузки оборудования является линейной. Ограничения и критерий оптимальности выражены в ней линей-ными функциями, т.е. функциями, в которые переменные входят в пер­вой степени.

Экономический смысл линейности соответствует предположению, что затраты производственных факторов пропорциональны результатам. Та­кое предположение лишь приближенно отражает реальную действитель­ность и основано на ряде допущений. Например, в рассмотренной нами модели учитывалось лишь станочное время и не принимались во внима­ние подготовительно-заключительные операции; прибыль на единицу детали считается не зависящей от количества изготовляемых деталей и т.д. Все же линеаризация реального процесса вполне допустима во многих практически важных случаях. Она существенно облегчает реше­ние задач оптимизации методом линейного программирования, приспо­собленным к различным классам ограничений и располагающим алгорит­мами их решения с помощью ЭВМ.

2.1. Приближенные числа

В ЭВМ срабатывают числа, которые записаны в формах с фиксиро­ванной и плавающей точками.

Десятичные числа с фиксированной точкой - это привычная нам форма записи чисел: 5; 10; 1.62 и т.д. Здесь вместо запятой ста­вится точка.

Как известно, множество целых чисел бесконечно. Однако ЭВМ из-за ограниченности ее разрядной сетки может оперировать лишь с некоторым конечным подмножеством этого множества. Так, для многих ЭВМ, например для микроЭВМ , целые числа лежат в диапазоне от 32768 до 32707.

При решении научно-технических задач в основном используются действительные (вещественные) числа. Для их представления использу­ется форма с плавающей точкой. Десятичное число x в этой форме записи имеет вид

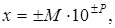
где М и P соответственно мантисса и порядок. Так число 273,9 можно записать в виде 273.9 ×10⁰; - 2739×10^-1; -2.739×10²; -.2739×10³. Последняя запись - нормализованная форма числа с пла­вающей точкой. Таким образом, если представить мантиссу числа в виде M = 0.a₁a₂a₃...a_n , то при a₁≠0 получаем нормализован­ную форму числа с плавающей точкой.

Подмножество действительных чисел для ЭВМ не является бесконеч­ным: оно конечно и определяется разрядностью k, а также границами порядка P₁≤P₂ (P₁≤P≤P₂) , Можно показать, что это подмножество содержит

2(a-1)(P₂- P₁+1)a^k-1+1 чисел.

Так, для микроЭВМ "Нейрон" диапазон действительных чисел

0.5877471×10^-38 =<x<=1701412×10³²

границы порядка P₁ и P₂ определяют ограниченность действительных чисел по величине, а размерность k - дискретность распределения их на числовой оси.

Например, в случае десятичных чисел при четырехразрядном пред­ставлении все значения, находящиеся в интервале между числами 0,2851 и 0.2852, представляются числом 0.2851 (при отбрасывании остальных разрядов без округления). Разность между двумя соседни­ми значениями равна 1 последнего разряда. Числа меньше этой разно­сти воспринимается как машинный нуль.

Таким образом, ЭВМ оперирует с приближенными значениями дейст­вительных чисел. Мерой точности приближенных чисел является погреш­ность.

2.2. Относительная и абсолютная погрешности

При решении задач приходится иметь дело с различными видами оши­бок: ограничения, округления, исходной информация. Каждую из них можно представить в абсолютной и относительной формах.

Пусть x - истинное значение некоторой величины, а 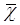- ее из­вестное приближение. Абсолютная погрешность равна разности истинно­го и известного приближения:

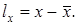
Относительная погрешность d_x определяется как отношение абсолют­ной погрешности к известному приближению:

Как правило, истинное значение x неизвестно, поэтому приближе­ние 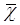задается предельной абсолютной погрешностью Dx:

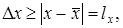(22)

Неравенство (22) дает возможность установить границы, в которых лежит истинное значение x:

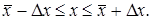
Абсолютная и относительные погрешности соизмеримы при значениях x, близких к единице.

Пусть x = 0.00001 и 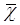= 0.000008, тогда 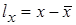=0.000002 и d_x = 0.25.

При значениях x, намного отличающихся от единицы, абсолютная и относительная погрешности сильно различаются:

Пусть x = 100000 и 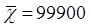, тогда lx= 100 и d_x = 0.0001.

 

2.3. Погрешности исходной информации и ошибки ограничения

Математическая модель, принятая для описания данного процесса или явления, может внести существенные погрешности, если в ней не учтены какие-либо важные исходные данные. Исходные данные часто являются основным источником погрешностей. Это так называемые не­устранимые погрешности, так как они не могут быть уменьшены иссле­дователем ни до начала решения задачи, ни в процессе ее решения.

Задача исследователя состоит в том, чтобы проанализировать иc-ходные данные для определения их точности, стремясь к тому, чтобы все исходные данные были примерно одинаковой точности.

Например, если длина детали l измеряется линейкой с миллиметро­выми делениями, то абсолютная погрешность, возникающая при измере­нии, не превысит 0,5 мм. В этом случае одновременно с длиной указы­вают границы измеряемой величины l ± 0,5 мм.

Многие числа (p, l) нельзя представить в виде конечной деся­тичной дроби. Ряд чисел при переводе из одной системы счисления в другую становится бесконечным. Например, 1/3 - бесконечная десятич­ная периодическая дробь; 0.2 в десятичной системе счисления при пе­реводе в двоичную систему счисления становится бесконечной периоди­ческой дробью 0.0011(0011). Поэтому, вычисляя с помощью ЭВМ сумму пяти чисел, каждое из которых равно 0.2 мм, мы не получим точно 1, так как ЭВМ оперирует числами в двоичной системе.

Ошибки ограничения определяются численными методами, используе­мыми при решении задач.

Если для вычисления значения синуса и используется степенной ряд

то, поскольку приходится ограничиваться конечным числом членов ряда, ошибка в вычислении будет определяться первым отброшенным чле­ном ряда. Такие ошибки называются ошибкой ограниче­ния, ибо она возникает в результате ограничения бесконечного математического процесса.

2.4. Ошибки округления

В инженерных расчетах используются в основном действительные числа, поэтому их сумма, разность, произведение и частное также являются действительными числами. Поскольку ЭВМ оперирует числами с конечным числом знаков и результат арифметической операции над вещественными числами округляется, то возникают ошибки округления.

Напомним, что действительное число с плавающей точкой мы рас­сматриваем в нормализованном виде, т.е. в виде правильной дроби, называемой мантиссой, умноженной на целую степень 10, называемую порядком:

Х=±М10^±Р, здесь М - мантисса, р - порядок:

0,1≤М<1.

При выполнении сложения или вычитания ЭВМ выравнивает порядки, т.е. сдвигает мантиссу меньшего по абсолютной величине числа впра­во или влево на столько порядков, на сколько пришлось увеличить или уменьшить порядок меньшего числа:

123 • 10³ + 0,453 • 10¹ = 0.123 • 10³ + 0.00453 • 10³ - 0.12753 • 10³.

Положим, что мантисса может быть представлена только тремя значащими цифрами. Представим полученную сумму в виде суммы двух ве­щественных чисел:

0.12753 • 10³ = 0,127 • 10³ + 0.53 • 10⁰.

Результат любого из четырех арифметических действий можно пред­ставить в общем виде:

x = ±M • 10^±Р + g • 10^Р-t,

где 0,1≤М<1; 0≤g<1; t - число значащих цифр в мантиссе (зна­чащими цифрами называют цифры, отличные от нуля). Существуют два способа округления результата арифметических операций:

1) g просто приравнивают к нулю;

2) к М прибавляется единица младшего разряда, если g по абсо­лютной величине больше или равно 0,5; если /g/<0.5, то М оста­ется без изменения.

Рассмотрим ошибку, появившуюся при первом и втором способах округления. При первом способе округления величина относительной погрешности будет

т.е. при этом способе округления относительная погрешность не за­висит от полученного результата, а определяется количеством знача­щих цифр в ячейке память ЭВМ.

При втором способе округленный результат записывается следую- щим образом:

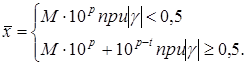
В этом случае абсолютная погрешность не превышает 0,5 • 10^p-t, а относительная - не будет превышать

Таким образом, во втором случае предельная ошибка округления меньше в два раза.

Как правило, известен лишь верхний предел возможной ошибки, по­этому при анализе точности вычисления на ЭВМ следует предполагать наихудший вариант: ошибки округления своему верхнему пределу.

2.5. Движение ошибок вычислительного процесса

В результат выполнения арифметических операций входит ошибка округления, и она должна учитываться при анализе результатов даль­нейших арифметических действий, выполняемых на ЭВМ.

Рассмотрим абсолютную и относительную погрешности каждой из че­тырех арифметических операций. Пусть числа x и y представлены так:

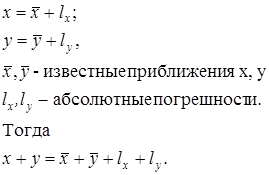
Абсолютная погрешность суммы

L_x+y=l_x+l_y

Аналогично запишем абсолютную погрешность разности;

L_x-y=l_x-l_y

При умножении

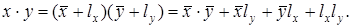
Величиной l_xl_y можно пренебречь в силу ее малости по сравне­нию с другими слагаемыми, тогда абсолютная погрешность произведе­ния будет

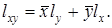
Запишем абсолютную погрешность частного, опуская преобразование:

а затем относительные погрешности каждой из арифметических операций

Эти формулы дают возможность проследить распространение ошибок. Абсолютные и относительные погрешности каждого из четырех действий можно рассматривать как функции приближенных значений исходных опе­рандов и их ошибок l_x, l_y,d_x,d_y. Ошибка округления в данной арифметической операции не учитывается и ее следует прибав­лять к погрешности арифметической операции.

Пример.

Вычислить

u = ((x+y)z+v)w,

где x,y,z,v,w - исходные числа, данные точно.

Вначале сложим числа x и y. Относительная погрешность сум­мы определится ошибкой округления и не должна превышать при втором

способе 0,5×10^-t+1, где t - число значащих цифр в мантиссе:

Далее

по условию

Следя за движением ошибки, получим

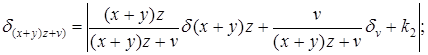
здесь k₂ - ошибка определения, возникающая при прибавлении V:

Так как dv = 0 по условию, то

Окончательно запишем:

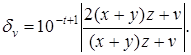
Окончательная погрешность dv возникла из-за ошибки округления в каждой из арифметических операций.

 

2.6. Граф вычислительного процесса

Существует более удобный способ анализа распространения ошибки в арифметических операциях. Последовательность операций в арифметическом выражении изображается с помощью так называемого графа [17].

Около стрелок графа пишутся, коэффициенты, позволяющие легко оп­ределить общую погрешность результата.

Граф следует читать снизу вверх, причем сначала выполняются операции одного горизонтального уровня.

Коэффициенты у стрелок пишутся по определенным правилам.

Если складываются два числа a и b, то у двух стрелок, входя­щих в кружок сложения, коэффициенты будут a/(a+b) и b/(a+b), как показано на рис. 6.

Аналогично при вычитании a/(a-b) и b/(a-b) получим граф, изображенный на рис. 7.

При умножении стрелки получают коэффициенты +1 (рис. 8).

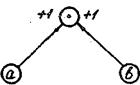
Рис. 8

При делении a/b стрелка, идущая от числа a, снабжается коэф­фициентом +1, а идущая от числа b - коэффициентом -1 (рис. 9)

Рис. 9

Смысл этих коэффициентов таков: относительная ошибка результата любой операции (кружка) входит в результат следующей операции, ум­ножаясь на коэффициент у стрелки, соединяющий эти две операции.

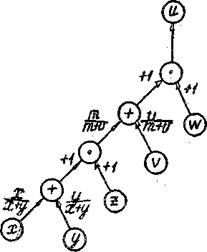Граф вычислительного про­цесса u=((x+y)z+v)w

показан на рис.10.

Рис. 10

Здесь при­нято обозначение m=(x+y)z.

Рекомендации для построения графа вычислительного процесса [17]:

1. При сложении и вычитании длинной последовательности чи­сел арифметические операции начинают с наименьших чисел.

2. Преобразуя формулы, сле­дует избегать вычитания двух приблизительно равных друг дру­гу чисел.

3. Следует по возможности уменьшить число выполняемых операций, ограничившись необхо­димым минимумом их.

 

2.7. Устойчивость. Корректность. Сходимость

Устойчивость. Рассмотрим погрешности исходных данных. Как по­казано выше, эти погрешности неустранимы и исследователь не может с ними бороться. Тем не менее нужно иметь представление об их вли­янии на точность окончательных результатов. Некоторые задачи весь­ма чувствительны к неточностям в исходных данных. Эта чувствитель­ность характеризуется так называемой устойчивостью. Пусть в резуль­тате решения задачи по исходному значению величины x находится значение искомой величины y. Если исходная величина имеет абсо­лютную погрешность Dx, то решение имеет погрешность Dy. Задача называется у с т о й ч и в о й по исходному параметру x, если решение y непрерывно от него зависит, т.е. малые приращения исходной величины приводят к малым погрешностям в результате рас­четов.

Отсутствие устойчивости означает, что даже незначительные пог­решности в исходных данных приводят к большим погрешностям в реше­нии или вовсе к невероятному результату. О таких неустойчивых задачах также говорят, что они чувствительны к погрешностям исходных данных.

Рассмотрим пример, приводимый Уилкинсоном [16]:

P(x)=(x-1)(x-2)(x-3)…(x-20)=x²⁰-210x¹⁹+…

Очевидно, что корнями этого многочлена будут X₁=1; X₂=2, …,X₂₀=20

Пусть один из коэффициентов вычислен с очень малой погрешностью, скажем, коэффициент - 210 увеличим на 2^-23 (около 10^-7). В резуль­тате вычислений даже с точностью до 11 значащих цифр получим такие корни:

X1	1.00	X9=8.92;
X2	2.00	X10,11=10.1±0.644 i ;
X3	3.00	X12,13=11.8±1.65 i ;
X4	4.00	X14,15=14.1±2.52 i ;
X5	5.00	X16,17=16.7±281 i ;
X6	6.00	X18,19=19.5±194 i ;
X7	7.00	X20=20.8.
X8	8.01

 

Таким образом, изменение коэффициента - 210 при X¹⁹ на 210¸10^-7 привело к тому, что половина корней стали комплексными.

Причина такого явления - неустойчивость самой задачи, хотя вычисление выполнено очень точно (11 разрядов), а погрешности округлений не могли привести, к таким последствиям.

Корректность. Задача называется поставленной корректно, если для любых значений исходных данных из некоторого класса ее решения существуют единственно и устойчиво по всем исходным данным.

Рассмотренный выше пример, приведенный Уилкинсоном [16], является некорректно поставленным. Применять для решения таких задач численные методы нецелесообразно.

В настоящее время развиты методы решения некоторых некорректных задач, так называемые методы регуляризации. Они основываются на замене исходной задачи корректно поставленной задачей, содержащей некоторый параметр, при стремлении которого нулю решение этой задачи переходит в решение исходной задачи.

Неустойчивость методов. Иногда при решении корректно поставленной задачи может оказаться неустойч