Система диагностики, использующая нечёткие правила.

Выводы

1. Анализ межотраслевого баланса дает комплексную характеристику процесса формирования и использования совокупного общественного продукта в отраслевом разрезе.

2. В основу схемы межотраслевого баланса положено разделение совокупного продукта на две части, играющие различную роль в процессе общественного воспроизводства, – промежуточный и конечный продукт.

3. Основной вопрос, возникающий в планировании производства на заданный период формулируется, как правило, следующим образом: при заданном векторе Y конечного потребления требуется определить необходимый объем валового выпуска, т.е. решить систему:

X – AX = Y, X ≥ 0. Условие неотрицательности X создает определенные трудности при исследовании вопроса о существовании решения системы.

4. Продуктивность модели Леонтьева полностью определяется величиной фробениусова собственного числа λ_A матрицы А коэффициентов прямых затрат.

5. Статическая модель Леонтьева может быть использована для рассмотрения вопрос использования и распределения трудовых ресурсов.

6. При моделировании межотраслевых связей важным является вопрос агрегирования нормативных показателей.

Рассмотренные до сих пор нечёткие выводы представляют собой восходящие выводы - от предпосылок к заключению. Они наиболее часто используются на практике.

В последние годы в диагностических нечётких системах начинают применятся нисходящие выводы. По существу это метод моделирования с помощью уравнения нечётких отношений.

Рассмотрим нисходящие нечёткий вывод на примере диагностической системы (рис 2).

Пусть - полное пространство предпосылок Х состоит из m факторов

- полное пространство заключений Y состоит из n симптомов

X = {x₁, x₂, … x_m};

Y = {y₁, y₂, … y_n}.

Рассмотрим упрощённую модель диагностики неисправности автомобиля при

m = 2, n = 3.

Х: х₁- неисправность аккумулятора;

х₂ – отработка машинного масла.

Y: у₁ – затруднения при запуске;

у₂ – ухудшение цвета выхлопных газов;

у₃ – недостаток мощности.

Между Х и Y существует нечёткое причинное отношение:

, .

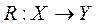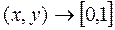Отношение R можно представить в виде матрицы:

R = [r_ij], i = 1…m;

j = 1…n, r_ij[0, 1], r_ij = x_i y_j.

Конкретные входы (предпосылки) и выходы (заключения) системы можно рассматривать как нечёткие множества А и В на пространствах Х и Y. Отношения этих множеств можно обозначить как

В = АR , где o - композиция нечётких выводов.

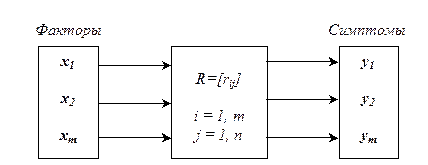
Рис. 2 – Система диагностики, использующая нечеткие правила.

Направление выводов является обратным к направлению выводов для правил. То есть, в случае диагностики:

Имеются: R - знание эксперта.

Наблюдаются: В - выходы или симптомы.

Задача: найти А - входы или факторы.

Пусть знание эксперта-автомеханика имеют вид:

Результат осмотра автомобиля оценивается как

В = {0.9/y₁, 0.1/y₂, 0.2/y₃}.

Требуется определить причину такого состояния:

найти А = {а₁/х₁, а₂/х₂},

т.е. определить значения степеней принадлежности а₁, а₂ каждого фактора х₁, х_2.

Решение:

В = АR ,

В = [0,9, 0,1, 0,2] ,

А = [a₁, a₂], тогда

 

[0,9 0,1 0,2] = [a₁, a₂] o ,

или в виде нечетких векторов-столбцов

Раскрывая (max-min)-композицию получим следующую систему уравнений:

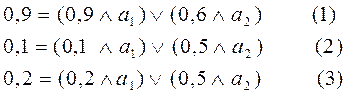
Систему из трех уравнений с двумя неизвестными необходимо решить относительно а₁ и а₂.

В уравнении (1) второй член правой части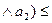 (0,60,6 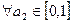. Поэтому он не оказывает влияния на левую часть, следовательно можно записать:

, следовательно

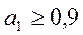. Подставив найденное решение в уравнение (2), получим :

;

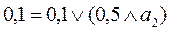0,5;

а_{2 .}

Формула (3) справедлива при данном решении

Таким образом, получаем решение: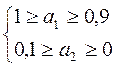

а₁ – параметр неисправности аккумулятора Вывод:

а₂ – параметр отработки машинного масла Лучше заменить аккумулятор.

На практике m и n принимают значения от нескольких единиц до нескольких десятков. Может использоваться нескольких правил композиции нечётких выводов.

В данном примере решение получено как значение на отрезке. В результате чего можно рассматривать максимальное решение [1 , 0,1] – {1/x₁, 0,1/x₂},

и минимальное решение [0,9 , 0] – {0,9/x₁, 0/x₂}.

В общем случае для композиции типа (max-min cвёртки) существует одно максимальное и несколько меньших решений.

На практике количество методов решения систем уравнений нечётких отношений значительно меньше, по сравнению с количеством методов прямого вывода по правилам.