Базис и координаты вектора

Линейно-независимые векторы образуют базис для какого-либо множества векторов, если любой вектор из этого множества может быть представлен в виде некоторой линейной комбинации этих векторов.

Поскольку любой вектор на плоскости может быть разложен по двум неколлинеарным векторам, а любой вектор в пространстве – по трем некомпланарным векторам, то любые два неколлинеарных вектора образуют базис на плоскости, а любые три некомпланарных вектора – базис в пространстве.

Пусть какая-нибудь тройка векторов e₁, e₂, e₃ образует базис в пространстве. Тогда любой вектор пространства можно разложить и притом единственным образом по этому базису:

a = a₁e₁ + a₂e₂ + a₃e₃.

Числа a₁, a₂, a₃ называются координатами вектора a в базисе векторов e₁, e₂, e₃ и будем обозначать

a = {a₁, a₂, a₃}.

Значение координат состоит в том, что операции над векторами сводится к действиям над числами. Пусть векторы a и b заданы своими координатами в одном и том же базисе:

a = {a₁, a₂, a₃} и b = {b₁, b₂, b₃}.

Тогда при сложении векторов будут складываться их соответствующие координаты, при умножении вектора на число все его координаты умножаются на это число:

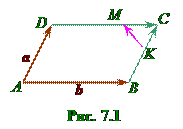Пример 7.1. В параллелограмме ABCD сторона BC разделена точкой K так, что 3|BK|=5|KC|, а сторона CD – точкой M так, что |CM|=4|MD| (см. рис.7.1). Разложить вектор по векторам и , или, по-другому, найти координаты вектора в базисе векторов a и b.

Решение. По правилу сложения векторов можно написать

Поскольку

,

,

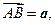
то

â

Пример 7.2. Даны три некомпланарных вектора a = {3;–2;1}, b = {–1;1;–2},
c = {2;1;–3}. Найти разложение вектора d = {11;–6;5} по базису a, b ,c.

Решение. Разложение имеет вид

d = aa + bb + gc.

Тогда

11e₁–6e₂+5e₃ = a(3e₁–2e₂+e₃) + b(–e₁+e₂–2e₃) + g(2e₁+e₂–3e₃)

или

(11–3a–b+2g)e₁ + (–6+2a–b+2g)e₂ + (5–a+2b+3g)e₃ = 0,

где e₁, e₂, e₃ – какой-то фиксированный базис. Поскольку этот базис состоит из линейно независимых векторов, то коэффициенты при этих векторах должны равняться нулю. Отсюда получаем систему линейных уравнений

Таким образом, искомое разложение имеет вид

d = 2a – 3b + c. â

Признак коллинеарности векторов в координатной форме примет следующий вид: два вектора a и b коллинеарны тогда и только тогда, когда пропорциональны их соответствующие координаты:

(7.4)

Пример 7.3. Коллинеарны ли векторы c₁ = 2a+b и c₂ = a–2b, если a={2;–2;4} и
b={–3;3;–6}.

Решение. Найдем координаты векторов c₁ и с₂:

с₁ = 2{2;–2;4} + {–3;3;–6} = {1;–1;2},

с₂ = {2;–2;4} – 2{–3;3;–6} = {8;–8;16}.

Из условия пропорциональности

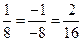
заключаем, что векторы c₁ и c₂ коллинеарны, причем . â