Линейная зависимость и независимость векторов

Если вектор b связан с векторами a₁, a₂, ... , a_n условием

b = k₁a₁ + k₂a₂ +... + k_na_n, (7.1)

то вектор b называется линейной комбинацией векторов a₁,a₂,...,a_n, или разложением вектора b по векторам a₁, a₂, ... , a_n. В связи с этим возникает вопрос: в каких случаях вектор можно разложить по заданным векторам? Ответ на этот тесно переплетается со следующим понятием.

Определение. Система векторов a₁, a₂, ... , a_n называется линейно зависимой, если найдется хотя бы одно не равное нулю число k₁, k₂ , ... , k_n, чтобы выполнялось равенство

k₁a₁ + k₂a₂ +... + k_na_n = 0. (7.2)

Если данное равенство может выполняться только при условии, что все числа k₁, k₂ , ... , k_n равны нулю, то такая система векторов называется линейно зависимой.

Из данного определения следует, что если система векторов линейно зависима, то, по крайней мере, один из них можно записать в виде линейной комбинации остальных. Например, если k₁¹0, то

.

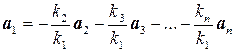Далее возникает вопрос: сколько в системе может быть линейно независимых векторов?

1) Признак коллинеарности векторов. Два ненулевых вектора a и b коллинеарны тогда и только тогда, выполняется равенство

a = kb, k ¹ 0. (7.3)

Отсюда следует, что в системе коллинеарных векторов может быть только один линейно независимый вектор, поскольку любые два коллинеарных вектора всегда линейно зависимы.

2) Необходимым и достаточным условием линейной зависимости трех векторов является их компланарность. Это означает, что в системе компланарных векторов может быть не более двух линейно независимых векторов. Поскольку два вектора линейно независимы тогда и только тогда, когда они неколлинеарны, то это означает, что любой вектор на плоскости можно разложить по двум неколлинеарным векторам.

3) Любые четыре вектора линейно зависимы. Это означает, что в системе векторов пространства может быть не более трех линейно независимых векторов. Поскольку три вектора линейно независимы тогда и только тогда, когда они некомпланарны, то отсюда следует, что любой вектор в пространстве можно разложить по трем некомпланарным векторам.

Вопросы. 1) Может ли быть линейно зависимой система, состоящая из одного вектора? 2) Может ли быть линейно независимой система векторов, содержащая нулевой вектор?