Потенциал объема
Рассмотрим потенциал объема
 (1)
(1)
где  - конечная область. Предположим, что плотность
- конечная область. Предположим, что плотность  ограничена и интегрируема в
ограничена и интегрируема в  . Интеграл (1) является собственным, если точка
. Интеграл (1) является собственным, если точка  лежит вне
лежит вне  . В этом случае функция
. В этом случае функция  непрерывна и имеет частные производные всех порядков. Эти производные могут быть получены дифференцированием под знаком интеграла, и
непрерывна и имеет частные производные всех порядков. Эти производные могут быть получены дифференцированием под знаком интеграла, и  удовлетворяет уравнению Лапласа
удовлетворяет уравнению Лапласа  вне области
вне области  . Покажем, что при стремлении точки
. Покажем, что при стремлении точки  в бесконечность по любому направлению функция
в бесконечность по любому направлению функция  стремится к нулю, так что
стремится к нулю, так что

где  .
.
Пусть начало координат принадлежит области  . Тогда
. Тогда 
или
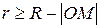 .
.
Обозначим через  - диаметр области
- диаметр области  . Тогда
. Тогда
 .
.
Будем считать, что точка  настолько удалена от начала координат, что
настолько удалена от начала координат, что  , т.е.
, т.е.  , тогда
, тогда  или
или  . Теперь
. Теперь
 ,
,
где
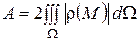 .
.
Таким образом, потенциал объема  есть гармоническая функция вне области
есть гармоническая функция вне области  .
.
Пусть теперь точка  лежит внутри области
лежит внутри области  . Тогда интеграл (1) будет несобственным. В силу ограниченности плотности
. Тогда интеграл (1) будет несобственным. В силу ограниченности плотности 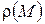 интеграл (1) сходится так, как
интеграл (1) сходится так, как
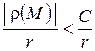 .
.
Кроме этого можно показать, что потенциал  и его производные первого порядка непрерывны во всем пространстве и эти производные могут быть получены дифференцированием под знаком интеграла.
и его производные первого порядка непрерывны во всем пространстве и эти производные могут быть получены дифференцированием под знаком интеграла.
Для существования производных второго порядков требуется наложить на плотность потенциала 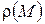 дополнительные ограничения. А именно справедливо утверждение:
дополнительные ограничения. А именно справедливо утверждение:
Теорема 1.Если плотность 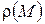 непрерывна в замкнутой области
непрерывна в замкнутой области  и имеет непрерывные производные первого порядка внутри
и имеет непрерывные производные первого порядка внутри  , то потенциал объема (1) имеет непрерывные производные второго порядка внутри
, то потенциал объема (1) имеет непрерывные производные второго порядка внутри  и удовлетворяет внутри
и удовлетворяет внутри  уравнению Пуассона
уравнению Пуассона
 .
.
Итак, если  , то уравнение Пуассона
, то уравнение Пуассона

имеет частные решение
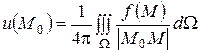 .
.