На основе МНК
Оценка параметров нелинейной эконометрической модели
Отметим, что совершенно аналогично случаю линейной зависимости находятся параметры функционала для нелинейных зависимостей – степенной, правой логарифмической, гиперболической, логарифмической гиперболической и обратной линейной. Во всех этих случаях следует перейти к другим переменным, относительно которых вид уравнения относительно параметров уже будет представлять линейную зависимость. При этом, конечно, из исходных данных следует получить матрицы данных для новых переменных.
Несколько по другому поступают в случае функции с постоянной эластичностью замены. Значения параметров 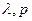 в нескольких альтернативных вариантах выбираются из концептуальных подходов. Затем для каждого такого набора значений
в нескольких альтернативных вариантах выбираются из концептуальных подходов. Затем для каждого такого набора значений 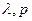 возведением уравнения зависимости
возведением уравнения зависимости
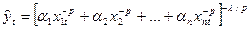 (10)
(10)
в степень  получается более простое соотношение относительно параметров
получается более простое соотношение относительно параметров 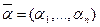 .
.
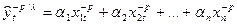 (11)
(11)
Теперь замена переменных
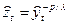 ,
, 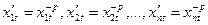 (12)
(12)
дает нам вид линейной зависимости
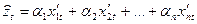 (13)
(13)
А для такой зависимости нахождение параметров по методу наименьших квадратов уже выше разобран. Надо только исходные данные перевести в данные для новых переменных. Выбор наиболее подходящей модели из нескольких альтернативных вариантов проводится на основе МНК прямым его применением, как было описано в самом начале этой лекции.
Еще сложнее происходит выбор параметров для экспоненциальной зависимости.
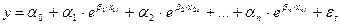 (14)
(14)
Если же параметры  уже как-то выбраны, то выбор параметров
уже как-то выбраны, то выбор параметров 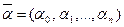 уже может быть осуществлен МНК.
уже может быть осуществлен МНК.
Классификация нелинейных регрессий.
Функциональную зависимость внутренней переменной от независимых факторов иногда называют регрессией, подчеркивая этим, что эта зависимость упрощенно отражает реальный процесс. Линейная регрессия, как уже отмечалось, имеет вид (4). А вот нелинейных регрессий довольно много. Их различают по виду и сложности. К нелинейным регрессиям первого класса относят нелинейные регрессии по включенным переменным. Параметры 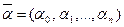 в эту зависимость входят линейно. К этому классу регрессий относятся правая логарифмическая, гиперболическая, логарифмическая гиперболическая, экспоненциальная зависимости, в виде многочлена по отдельным переменным и их линейные комбинации. Примером такой регрессии может служить многочлен от одной переменной в случае рассмотрения парных регрессий:
в эту зависимость входят линейно. К этому классу регрессий относятся правая логарифмическая, гиперболическая, логарифмическая гиперболическая, экспоненциальная зависимости, в виде многочлена по отдельным переменным и их линейные комбинации. Примером такой регрессии может служить многочлен от одной переменной в случае рассмотрения парных регрессий:
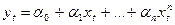 .
.
Ко второму классу нелинейных регрессий относятся модели нелинейные по оцениваемым параметрам. Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные.
Модели первого вида с помощью подходящих преобразований могут быть приведены к моделям линейного типа. К такому типу относятся, например, зависимости с постоянной эластичностью замены.
Если в степенной зависимости вероятностная составляющая учитывается как сомножитель
 (15)
(15)
то этот функционал так же относится к первому виду, так как переход к логарифмическим переменным сводит ее к линейной зависимости. Если же эта вероятностная составляющая учитывается как аддитивный член
 (16)
(16)
то этот функционал относится ко второму типу второго класса, эта модель внутренне нелинейная.
Ко второму виду зависимости относится и экспоненциальный функционал.
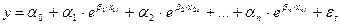 (17)
(17)
Модели внутренне нелинейные по параметрам могут и нередко используются в эконометрических исследованиях. Однако гораздо большее распространение получили модели, приводимые к линейному виду. Отметим, что именно для таких моделей решение реализовано в стандартных пакетах прикладных программ.
Из нелинейных функционалов, которые могут быть приведены к линейному виду, в качестве нелинейной регрессии широко используется степенная функция
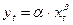 (18)
(18)
Это объясняется тем, что параметр 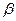 в ней является коэффициентом эластичности, показывающим, на сколько процентов изменится результат, если фактор изменится на 1%. Коэффициент эластичности в таких случаях определяется из общих концептуальных подходов. Коэффициент эластичности можно определять и при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру
в ней является коэффициентом эластичности, показывающим, на сколько процентов изменится результат, если фактор изменится на 1%. Коэффициент эластичности в таких случаях определяется из общих концептуальных подходов. Коэффициент эластичности можно определять и при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру 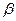 . Но не для всех процессов эластичность нужна, или она играет важную роль. Тем более, что практически часто эластичность не является постоянной величиной, а является сложной зависимостью, а иногда и вообще не существует.
. Но не для всех процессов эластичность нужна, или она играет важную роль. Тем более, что практически часто эластичность не является постоянной величиной, а является сложной зависимостью, а иногда и вообще не существует.