Алгоритмы с гарантированной оценкой точности
Задача минимизации суммарного штрафа за невыполнение директивных сроков
Пример применения метода ДП
Динамическое программирование (ДП) - продолжение

3.1. Минимизация взвешенной суммы моментов завершения обслуживания требований.
Рассмотрим задачуP//ΣwjCj,
где
P – обозначение системы параллельных приборов с одинаковой производительностью
Cj – момент завершения обслуживания требованияj
wj – весовой коэффициент, характеризующий относительную важность требованияj
В этой задаче расписание однозначно определяется разбиением множества требований на подмножества N1,..., Nm,
где требования множества Nl обслуживаются прибором l,
При этом достаточно ограничиться рассмотрением расписаний, в которых требования каждого подмножества упорядочены по правилу SWPT, т.е. по неубыванию значенийpj/wj. Это можно доказать при помощи перестановочного приема.
Приведем приближенный алгоритм решения задачиP//ΣwjCj, для которого имеются гарантированная оценка точности.
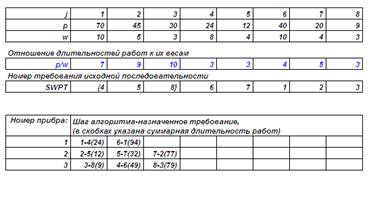
1. Перенумеруем требования в порядке SWPT так, что p1/w1 < … < pn/wn.
Далее будем последовательно, начиная с 1-го назначать требования приборам 1, .., n, пусть требования 0, … k, где 0 – фиктивное требование, соответствующее начальной ситуации, k < n, уже назначены.
2. Требование k + 1 назначается тому прибору l, сумма длительностей обслуживания ранее назначенных требований которого минимальна.
Т.е. если
Pl - сумма длительностей обслуживания требований, назначенных на прибор l, где l = 1, … , m.
то прибор l, выбирается исходя из условия Pl = min1<h<m Ph.
Назначаем требование k +1 на приборl
3. Еслиk+1=n, т.е все требования назначены - прекращаем процесс, иначе переходим к назначению тр-ия k+2.
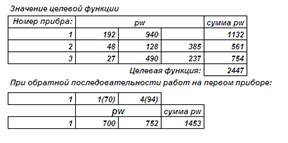
Заметим, что полученное про мощи алгоритма значение целевой функции является, в общем случае, оценкой сверху точного решения. Данный алгоритм относится к категории приближенных с гарантированной оценкой точности. Для него известна оценка величины ΔН=Fh/F* (где Fh – реш. посредством алгоритма, F* - точ. реш.).
Рассмотрим пример задачи P//ΣwjCj.
3 параллельно работающих станка обрабатывают 8 изделий. Изделия поступили на линию одновременно и требуют специальных условий хранения при пребывании на линии. Стоимость хранения изделия j в единицу времени wj и длительность его обработки pj указаны в таблице. Найти расписание, минимизирующее суммарную стоимость хранения изделий.
3.2. Минимизация числа используемых приборов
Рассмотрим задачу P/dj=d/Cj ≤ dj
d≥max pj, для j=1…т, а также m=n
Требуется отыскать минимальное число приборов и соответствующее расписание, при котором все требования будут обслужены к заданному директивному сроку d.
* * *
Обозначим Rl – резерв времени прибора l, то есть разницу между d и суммарной длительностью работ, уже назначенных на прибор l.
Обозначим π некоторую перестановку всех требований.
* * *
Для данной задачи известно 4 алгоритма с гарантированной оценкой точности. Вначале первому прибору назначается фиктивная работа p0.
На k-м шаге (k=1, …,n) для назначения выбирается требование, находящееся на месте k перестановки π.
- для первого алгоритма оно назначается на прибор с наименьшим номером l, при условии, что для прибора имеется достаточный резерв времени для выполнения требования без нарушения директивного срока.
- для второго алгоритма оно назначается на прибор с наименьшим достаточным резервом времени для выполнения требования без нарушения директивного срока.
Для третьего и четвертого алгоритма предполагается, что в перестановке π требования расположены в порядке LPT невозрастания значений pj, а назначения работ требованиям осуществляются также, как и в первом и втором алгоритмах.