Многофакторный линейный регрессионный анализ

Лекция 6

 

Пусть производятся наблюдения за системой, на входе которой действует k контролируемых независимых переменных x_i, i=l,...,k, (например, температура, давление, время протекания химического процесса, состав инградиентов и т. п.). На выходе системы ее состо­яние определяется выходной переменной у. Для определения взаимос­вязи между входными и выходной переменными проводится N наблюдений за системой в точках с координатами х¹, х²,...,х^N где . Результаты наблюдений представлены в виде вектора наблюдений

В каждой точке хⁱ в общем случае может быть проведено n_i наб­людений, в результате которых получены значения . Тогда в ка­честве результата наблюдения в точке хⁱ будем использовать значение 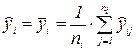, взятое с весом w_i = n_i с ошибкой .

Тогда , где - ошибка наблюдения (независимая случайная величина с 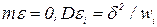). Примем, что уравнение регрессии - линейная функция вида

М[у/х] = b₀ + b₁x₁ + b₂х₂ +...+ b_kx_k.

Необходимо найти такие значения коэффициентов регрессии b_i i=0,...,k. чтобы полученное уравнение наилучшим образом отражало результаты наблюдений. Для нахождения коэффициентов b_i будем ис­пользовать МНК, минимизируя взвешенную сумму квадратов рассогласований между результатами наблюдений и уравнением регрессии:

, где

Запишем задачу в векторной форме, добавив к входным перемен­ным x_i I=1,2,...,k для удобства еще один столбец х₀, состоящий из одних единиц:

Обозначим:

- вектор столбец,

- вектор столбец,

- вектор столбец,

- весовая матрица.

Уравнение регрессии запишется в виде Y=X В , а взвешенная сум­ма квадратов отклонений в векторной форме:

где W = [ w_ij ], i, j=1,2,...,N - весовая матрица.

В качестве весовой матрицы W на практике наиболее часто ис­пользуется матрица W=К_y^-1 - матрица коэффициентов корреляции ре­зультатов наблюдений), т.е. обратная корреляционной матрице ре­зультатов наблюдений. В этом случае МНК-оценки коэффициентов b_i являются эффективными. Если результаты наблюдений независимы, то весовая матрица - диагональная. Если результаты наблюдения незави­симые и равноточные, то весовая матрица является единичной.

 

4.1. Нормальные уравнения МНК и оценки коэффициентов регрессии

 

Запись взвешенной суммы квадратов отклонений в векторной фор­ме вида 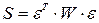, представляет собой квадратичную форму. Найдя для нее вектор частных производных и приравняв его нулю, получим:

Отсюда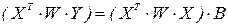

Это есть нормальные уравнения МНК, записанные в матричной форме, а их решения В называются МНК - оценками коэффициентов рег­рессии.

Если ранг матрицы X равен (k+1), то матрица невырож­денная и уравнения имеют единственное решение:

Если ранг матрицы X меньше (k+1), то решение не единственное, т. е. для получения оценок всех коэффициентов регрессии число неза­висимых наблюдений N должно быть не меньше числа оцениваемых пара­метров (k+1).

Матрица называется информационной. Матрица называется дисперсионной.

На практике кроме модели вида часто используется рег­рессионная модель вида y(b,x)=b₀f₀(x)+b₁f₁(x)+...+b_kf_k(x), где f_i(x) - известные функции, f(x)=[f₀(x),f₁(x),...,f_k(x)]^T. При этом уравнение регрессии остается линейным относительно коэф­фициентов регрессии b_i i=0, ...,k и в векторной форме запишется в виде Y = FB, где

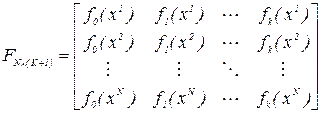
Здесь вместо матрицы X используется матрица F, т.е. на реше­ние влияет и вид модели у=(b,х). Решение имеет вид и соответственно матрица - информа­ционная, - дисперсионная. В остальном запись всех выра­жений не меняется.

 

4.2. Анализ оценок коэффициентов регрессии

 

Как уже говорилось ранее, оценки коэффициентов линейной рег­рессии, найденные по МНК являются несмещенными, т.е. .

Для анализа взаимосвязи оценок и величины их рассеивания не­обходимо найти ковариационную матрицу оценок коэффициентов регрес­сии. Можно показать, что

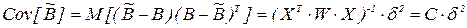
Как видно, в общем случае оценки коэффициентов линейной рег­рессии - зависимые случайные величины. Для того чтобы они были не­зависимы, необходимо, чтобы информационная матрица была диагональной. Это условие выполняется, если столбцы матрицы X (или матрицы F) попарно ортогональны, т. е.

Тогда элементы ковариационной матрицы будут равны:

Здесь С_ii- диагональный элемент дисперсионной матрицы .

Получение статистически независимых оценок существенно упро­щает дальнейший их анализ и широко применяется на практике при проведении активного эксперимента на ортогональных планах.

Из ковариационной матрицы можно получить дисперсии оценок ко­эффициентов

 

4.3. Анализ качества уравнения многомерной линейной регрессии

 

Для проведения статистического анализа качества полученной оценки уравнения регрессии составим очевидное тождество:

где y_i - результат наблюдения в точке х¹; - значение у, вы­численное по уравнению регрессии (оценки); - взвешенное среднее

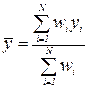
Возведём обе части тождества в квадрат, просуммируем с весом wt и получим (смешанные произведения, как и ранее, сокращаются):

Обозначив, как и ранее (см п.3.2), получим основное тождество вариаций S06ui = S2 + S3. Здесь в первой части отсутствует слагае­мое Sb характеризующее отклонение наблюдений в точке Xi от сред­него в этой точке, так как в каждой точке проводится только одно наблюдение. Величина S2 характеризует отклонение наблюдений от ли­нии регрессии, a S3 - за счет регрессии:

Таблица дисперсионного анализа (табл. 4. I) имеет следующий вид.