ОЦЕНИВАНИЕ ПАРАМЕТРОВ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ.

Пусть в результате n независимых наблюдений над системой при одних и тех же значениях контролируемых факторов получено n значений скалярной случайной величины Y 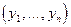, характеризующей результат работы системы ( случайная выборка объема n из генеральной совокупности ). Любая функция от этих значений S = S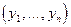называется статистикой и также случайна. Если статистика используется в качестве приближения для параметра закона распределения, то полученное с помощью этого выражения S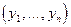значение называется оценкой параметра. При выборе зависимости, по которой вычисляется оценка, необходимо, чтобы она ( оценка ) отвечала требованиям состоятельности, несмещенности и эффективности.

1). Оценка 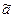параметра 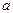состоятельна, если она сходится по вероятности к оцениваемому параметру :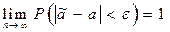

Это условие выполняется, если с ростом 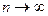дисперсия оценки .

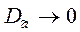2). Оценка 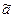параметра 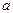несмещенная, если M[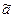] = 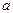, иначе оценка смещенная.

3).Несмещенная оценка 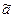называется эффективной, если ее дисперсия минимальна. 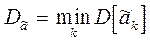, где k - номер вида статистики.

Для определения оценок наиболее широко используются метод моментов и метод максимального правдоподобия.

В основе метода моментов лежит принцип равенства статистических ( выбо- рочных ) и действительных ( неизвестных ) моментов распределения. Число приравниваемых моментов равно числу оцениваемых параметров. При этом статистические моменты определяются аналогично моментам дискретного распределения.

В соответствии с методом максимального правдоподобия строится функция правдоподобия L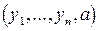как функция от значений случайной величины Y в выборке и параметра 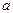. В качестве оценки параметра 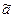берется такое значение аргумента 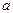, которое обращает функцию L( Y, a ) в максимум.

Среди наиболее распространенных оценок обычно используют оценки матетати- ческого ожидания и дисперсии.

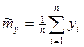
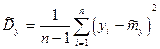
Эти оценки состоятельные и не смещенные. Однако в общем случае не являются эффективными. Для получения представления о точности получаемых оценок используются так называемые “интервальные“ оценки, представляющие собой доверительный интервал 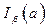, в который с заданой доверительной вероятностью b попадает действительное значение параметра а .

Для построения доверительного интервала для параметра а необходимо знание закона распределения его оценки.

В ряде случаев он может быть найден. Так при большом n ( > 120 ) закон распределения 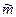стремится к нормальному при любом виде закона распределения случайной величины Y.

Доверительный интервал 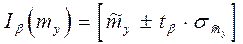, где

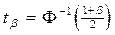
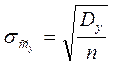, или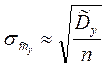

При малых n значение 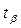берется из нормального закона распределения только если известно значение Dy. В противном случае - из t-распределения Стьюдента при ( n-1 ) числе степеней свободы.

Закон распределения оценки дисперсии 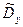известен только если сама случайная величина Y распределена по нормальному закону. В этом случае 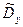распределена по 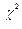- распределению с числом степеней свободы ( n-1). И доверительный интервал для дисперсии имеет вид :

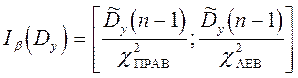
где 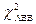, 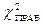ищутся из 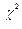-распределения с ( n-1 ) степенью свободы с помощью таблиц.

 

 

 

· ·

 

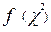
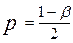
В остальных случаях для построения кривых распределения оценок и соответственно доверительных интервалов могут использоваться численные методы (например, бутстреп-методы) [8]. Следует заметить, что для оценок, получаемых на основании статистических моментов при закон распределения среднего арифметического функции стремится к нормальному практически при любых законах распределения случайной величины . Необходимо только большое число наблюдений, что при исследовании реальных систем не всегда выполняется. При проведении статистического анализа широко используется математический аппарат статистической проверки гипотез.