Основные понятия теории вероятностей

СТАТИСТИЧЕСКОЕ ОПИСАНИЕ СВОЙСТВ ИДЕАЛЬНОГО ГАЗА.

Заключение

В период раздробленности на Руси продолжалось развитие институтов раннефеодального государства, но не в форме единого государства, а в форме разрозненных крупных, средних и мелких государств.

В этот период утверждается новая форма правления – республика: Новгородская, Псковская, менее известная Вятская. Некоторые исследователи считают Галицко-Волынское княжество аристократической республикой.

Крупные законодательные акты периода раздробленности сохранились только в феодальных республиках: Новгородская судная грамота и Псковская судная грамота.

Развитие Руси в период раздробленности было осложнено завоеванием большей части ее территории монголо-татарами и 250-летним монгольским господством.

 

Для изучения макросистем применяют статистические методы, использующие понятия и величины, относящиеся не к отдельным частицам, а к большим совокупностям частиц. Подробно о статистическом описании систем и теории вероятностей можно прочитать в [2,4,12,14,16].

Многие законы молекулярной физики, удобно трактовать, пользуясь понятием вероятности. К этому понятию прибегают, когда речь идет о случайных событиях.

Случайным событием называют такое событие, которое при некоторых условиях может произойти или не произойти.

Относительной частотой случайного события называют отношение числа nпоявления данного события к общему числу Nпроведённых испытаний, в каждом из которых могло проявиться или не проявиться данное событие.

Например, при одинаковых условиях было произведено три серии бросания монет: в первой серии было 10 бросаний, число монет, упавших орлом вверх, равно 4; во второй серии было 20 бросаний, число монет, упавших орлом вверх, равно 12; в третьей серии было 12 бросаний, число монет, упавших орлом вверх, равно 6. Событие - падение монеты орлом вверх. Относительная частота события в сериях будет: в первой серии 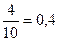, во второй серии , в третьей серии .

Данный пример, а также другие наблюдения различных явлений показывают, что, если число испытаний невелико, то относительные частоты появления события в каждой серии могут существенно отличаться одна от другой. Если же число опытов в сериях велико, то относительные частоты отличаются мало. Опыт показывает, что существует такое число w, называемое вероятностью случайного события, что относительные частоты события при большом числе испытаний мало отличаются от этого числа.

Вероятностью w случайного события, называется предел, к которому стремится отношение числа опытов, приводящих к его осуществлению, к общему числу опытов при беспредельном увеличении последнего:

(3.1)

Вероятность случайного события может изменяться в следующих границах .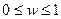

Вероятность невозможного события равна нулю, вероятность достоверного события равна единице.

Два события А и В называют несовместимыми или непересекающимися, если при проведении некоторого испытания они не могут произойти одновременно.

Суммой, или объединением, двух событий называют наступление одного из двух событий А или В и записывают в виде:

С = А+В или (Здесь - знак объединения).

Вероятность наступления одного из несовместимых событий А или В определяется законом сложения вероятностей

(3.2)

Пример. Вероятность нахождения частицы в объёме V₁ равна w₁ =0,3 , вероятность нахождения её в объёме V₂ равна w₂ =0,2 . Какова вероятность нахождения частицы в любом из этих объёмов или в объёме V₁ или в объёме V₂ ?

Решение.Частица не может находиться одновременно сразу в двух объёмах, эти события несовместимы, следовательно

w = w₁ + w₂ , w = 0,3+0,2 = 0,5

Два события называются независимыми, если наступление одного из них не влияет на вероятность наступления другого.

Произведением, или пересечением, двух событий называют одновременное или последовательное наступление обоих событий А и В и записывают в виде:

С = А^.В или (Здесь - знак пересечения).

Для двух независимых событий выполняется закон умножения вероятностей.

(3.3)

Пример. Вероятность обнаружения частиц одного сорта в объёме V₁ равна w₁ = 0.8 , вероятность обнаружения их в объёме V₂ равна w₂ = 0,5. Эти события независимы. Какова вероятность обнаружить частицы данного сорта и в объёме V₁ и в объёме V₂ одновременно?

Решение. Так как данные события независимы, то можно использовать теорему умножения вероятностей: w₁ =0,8 , w₂ =0,5, тогда w = 0,8^.0,5 =0,4. В 40% будут наблюдаться одновременно эти два события.

В физике многие микропараметры являются случайными величинами, поэтому необходимо представление о среднем значении случайной величины. Среднее арифметическое значение случайной величины тесно связано с вероятностью. Пусть N – число наблюдений величины Х. Пусть в N₁ случаях величина Х имеет значение Х₁ , в N₂ случаях – Х₂ и так далее. Среднее арифметическое значение Х будет равно:

(3.4)

Так как , то можно записать среднее значение случайной величины Х через относительные частоты

(3.5)

При очень больших N относительная частота мало отличается от вероятности. Среднее арифметическое значение случайной величины называют в этом случае математическим ожиданием и записывают в виде:

(3.6)

Кроме среднего значения случайной величины, важно знать насколько сильно отличаются её значения от среднего. Для характеристики разброса значений случайной величины от среднего используют среднеквадратичное отклонение от среднего или стандартное отклонение. При большом числе наблюдений стандартную ошибку можно определить по формуле:

(3.7)

Стандартная ошибка имеет те же единицы измерения, что и случайная величина и показывает интервал, в котором оказывается случайная величина.

Другой характеристикой разброса значений случайной величины от среднего является дисперсия σ², равная квадрату стандартной ошибки. Она отражает «площадь» разброса случайной величины и измеряется в квадратных единицах измерения случайной величины.

Если явления характеризуются непрерывно меняющимися величинами, то определение вероятности по формуле (3.1) не имеет смысла. Например, не имеет смысла спрашивать, какова вероятность того, что скорость частицы равна 10 м/с, так как скорость - непрерывная случайная величина и может принимать любые значения, сколь угодно мало отличающиеся от заданной. Множество событий в таком случае не является счётным, и их вероятностное описание осуществляется с помощью плотности вероятности. Рассмотрим понятие плотности вероятности на физическом примере. Пусть в некотором сосуде находится газ. При различных актах наблюдения молекула оказывается в различных точках. В этом случае всё пространство (в том числе и вне объёма сосуда) делят (см. [2]) на небольшие объёмы DV_i (i = 1,2,3,..). Число таких объёмов бесконечно. Число актов наблюдений N. При каждом акте наблюдения молекула окажется обнаруженной в одном из объёмов DV_i . Пусть при N актах наблюдений (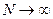) молекула обнаружена N_i раз в объёме DV_i . Тогда вероятность обнаружения молекулы в объёме DV_i равна . Внутри сосуда эта вероятность даже при равных объёмах различна (не постоянна), зависит от объёма DV_i . Поэтому для определения вероятности нахождения молекулы в объёме DV_i используют понятие плотности вероятности, определяя её как предел отношения вероятности нахождения частицы в объёме DV_i к величине этого объёма, при стремлении последнего к нулю:

(3.8)

Здесь x, y, z – координаты точки, к которой стягивается бесконечно малый объём. Таким образом, плотность вероятности это вероятность нахождения молекулы в бесконечно малом объёме вблизи некоторой точки, отнесённая к этому объёму; то есть она определяется так же, как и другие «плотности». Для одномерного случая:

(3.9)

Здесь х – координата точки, к которой стягивается бесконечно малый интервал Dх_i . Вблизи разных координат плотность вероятности может быть различной. Если изобразить графически распределение плотностей вероятностей, то кривая зависимостибудет называться кривой распределения плотностей вероятностей или дифференциальным законом распределения.

Если произвести N наблюдений, то в бесконечно малом объёме dV в окрестностях точки (x, y, z) молекула будет обнаружена в dN случаях:

или

Для одномерного случая:

(3.10)

Поскольку число молекул очень велико, 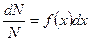имеет смысл вероятности нахождения молекулы вблизи точки с координатой x в интервале dx.

Если подсчитать число случаев N(V₁) обнаружения молекул в конечном объёме V₁ , то оно будет связано с плотностью вероятности следующим образом:

Вероятность быть обнаруженной в объёме V₁ для молекулы определяется формулой:

(3.11)

На рисунке 3.1, где изображено дифференциальное распределение случайной величины Х, вероятность частицы быть обнаруженной в интервале Dx вблизи некоторого значения x (одномерный случай) численно равна площади заштрихованной криволинейной трапеции. Знание плотности вероятности позволяет найти вероятность для любой области, в которой плотность определена. Поскольку вероятность для непрерывной случайной величины определяют через плотность вероятности, то и среднее значение непрерывной случайной величины определяют тоже через плотность вероятности. Для непрерывной случайной величины x , которая может принимать любые значения в интервале от 0 до a , среднее значение можно определить по формуле: .

Усреднение можно проводить по ансамблю или по времени [2,4,5,16].

Возьмём очень большое число N _a совершенно одинаковых сосудов с одинаковым числом молекул N в каждом из них. Сосуд с заключёнными в нём N молекулами можно назвать статистической системой. Совокупность статистических систем называется статистическим ансамблем. Вычислить среднее по ансамблю значение 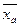некоторой случайной величины x , связанной с молекулой, можно по формуле:

,

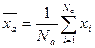где N _a – число систем в ансамбле, x_i – значение случайной величины, характеризующей молекулу в i – той системе ансамбля. При большом N _a , как показано в [2], среднее по ансамблю равно математическому ожиданию случайной величины х.

Вычислить среднее по времени значение 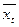некоторой случайной величины х в одной из систем ансамбля можно, проследив за ней в течение очень большого промежутка времени. Тогда 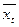можно вычислить по формуле:

В 1871 году Л. Больцман высказал эргодическую гипотезу, согласно которой среднее по ансамблю равно среднему по времени . Доказательство справедливости этой гипотезы до настоящего отсутствует.

Кроме дифференциального распределения некоторой случайной величины х, используют понятие интегрального распределения этой величины.

Пусть f(x) есть распределение плотности вероятности некоторой случайной величины х, которая может принимать любые значения (), тогда функция F(x) называется функцией распределения вероятностей или интегральным законом распределения. Значение F(x) , определяемое по формуле:

, (3.12)

показывает вероятность того, что случайная величина Х не превышает значения x.

На рис.3.2 (б) представлен вид интегрального распределения, соответствующий дифференциальному распределению, изображённому на рис.3.2(а). Заштрихованная часть на рис 3,2 (а) равна значению F(x) и означает вероятность того, что случайная величина Х не превышает значения х. На рис. 3.2(б) эта вероятность равна ординате точки А.

 

 

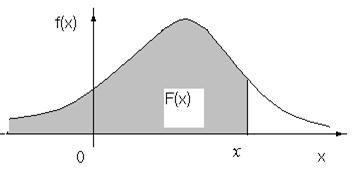
Рис.3.2 а

 

Рис.3.2 б

Из рис.3.2 (б) видно, что при значение . Это определяется условием нормировки: . Для трёхмерного случая:

(3.13)

Условие нормировки можно пояснить на примере всё тех же частиц газа в пространстве. Если выбрать объём, охватывающий всё пространство, то при каждом испытании частица окажется в какой-то точке пространства (факт существования частицы) и, следовательно, . Вероятность найти частицу будет равна единице:

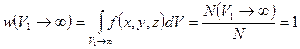
Вероятность попадания случайной величины Х в заданный интервал равна приращению функции распределения на этом интервале:

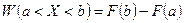или

Графически это изображено на рис. 3.3, где вероятность попадания случайной величины x в заданный интервал численно равна площади криволинейной трапеции в интервале.

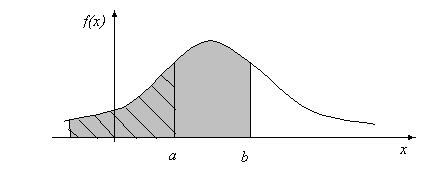
Рис.3.3