Уравнение состояния для конденсированных сред
Жидкости и твёрдые тела, в отличие от газов, имеют собственный объём и называются конденсированными средами. Объём определяется размерами молекул и силами молекулярного взаимодействия. Он слабо меняется в зависимости от давления и температуры. Поскольку размеры молекул и межмолекулярные силы специфичны для каждой системы, то универсального уравнения состояния для конденсированных сред не существует.
Для чистых сред соотношение между объёмом, температурой и давлением можно выразить через коэффициент объёмного расширения β и коэффициент изотермического сжатия Кт (изотермическую сжимаемость). Коэффициент объёмного расширения β выражает относительное изменение объёма при изменении температуры на 1 К при постоянном давлении и определяется формулой:
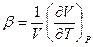 (6.30)
(6.30)
Коэффициент изотермического сжатия КT показывает относительное изменение объёма при изменении давления на единицу величины при постоянной температуре и определяется формулой:
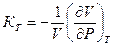 (6.31)
(6.31)
Если объём рассматривать как функцию от давления и температуры V(P,T), то дифференциал объёма будет определяться формулой:
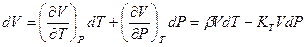 (6.32)
(6.32)
Уравнение (6.23) можно считать уравнением состояния конденсированных сред в дифференциальной форме. Проинтегрировав его по температуре и давлению можно получить уравнение состояния в интегральной форме.
Для твёрдых тел и жидкостей β и Кт малы. Для жидкостей β ~ 10 – 3 ÷10 – 4 К – 1 , Кт ~ 10 – 10 Па – 1 ; для воды β = 2,1*10– 4 К – 1, Кт = 4,96*10 – 10 Па – 1.
Отличительной особенностью конденсированных сред является слабая зависимость химического потенциала, энтропии и энтальпии от давления, следовательно, их можно считать функциями температуры для данного количества вещества. Если энтропию рассматривать как функцию давления и температуры S(P,T), то дифференциал энтропии (или приращение энтропии) будет иметь вид:
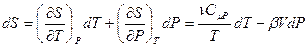 (6.33)
(6.33)
В интегральной форме:
 (6.34)
(6.34)
Так как β и V слабо изменяются в зависимости от давления, третье слагаемое можно записать в виде произведения: V β P . При давлениях Р~ 105 ÷106 Па этот член мал. Для воды он приблизительно равен 3,6.10 – 3 Дж/(моль . К), молярная теплоёмкость воды при этих условиях приблизительно равна 75 Дж/(моль . К). При нормальных условиях энтропия одного моля воды равна 70 Дж/К. Подобно тому, как мы получили выражения (6.32 - 6.34), можно получить и другие термодинамические функции.