Идеальная МДП-структура
МДП–структура
Если на окисел, покрывающий поверхность кристалла, нанести металлический электрод (затвор), то, изменяя его потенциал относительно объема кристалла, возможно изменять величину заряда в приповерхностной области полупроводника и, соответственно, её проводимость. Этот эффект положен в основу целого ряда полупроводниковых устройств, среди которых самое известное – МДП-транзистор.
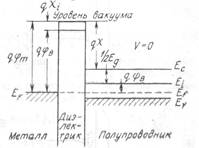
Рассмотрим идеальный МДП-конденсатор, энергетическая диаграмма которого представлена на рис. 1.

| 
|
| Рис. 1 |
Состояние носителей в разнородных материалах (металл – диэлектрик - полупроводник) можно сравнить, используя понятие нулевого потенциала, то есть принимая потенциал какой-либо точки (например, потенциал вакуума) за нуль (рис. 1). Тогда для перевода электрона со дна зоны проводимости полупроводника в вакуум без сообщения ему скорости потребуется энергия q·χ, равная:
 . .
| (1) |
Энергия q·χ есть энергия электронного сродства, χ.- сродство к электрону полупроводника. Если энергию электрона отсчитывать от энергии Ферми, а не от 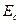 , используют понятие термоэлектронной работы выхода или просто работы выхода Φ:
, используют понятие термоэлектронной работы выхода или просто работы выхода Φ:
 . .
| (2) |
Таким образом, работа выхода равна разности между энергией покоящегося электрона в вакууме у поверхности образца полупроводника и уровнем Ферми в данном полупроводнике.
На границе металл-диэлектрик, диэлектрик-полупроводник, а в отсутствии диэлектрика на границе металл-полупроводник возникает контактная разность потенциалов:
 . .
| (3) |
Для случая «идеальной» МДП-структуры делается ряд допущений:
1.Разность работ выхода между металлом затвора и диэлектриком, диэлектриком и полупроводником, равна нулю или для потенциалов:
для n-типа: 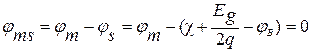 ,
для p-типа: ,
для p-типа:  . .
| (4) |
Здесь 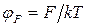 – потенциал уровня Ферми,
– потенциал уровня Ферми,  - разность между уровнем Ферми F и положением уровня Ферми в собственном полупроводнике Ei.
- разность между уровнем Ферми F и положением уровня Ферми в собственном полупроводнике Ei.
Условие означает, что в отсутствие внешнего напряжения энергетические зоны полупроводника не изогнуты (состояние плоских зон).
2. В диэлектрике и на границах раздела металл-диэлектрик и полупроводник-диэлектрик нет никаких зарядов, т.е. диэлектрик не имеет дефектов. При любых смещениях в структуре могут существовать только заряд в ее полупроводниковой части и равный ему заряд противоположного знака на металлическом электроде, отделенном от полупроводника слоем диэлектрика.
3. Диэлектрик является идеальным изолятором.
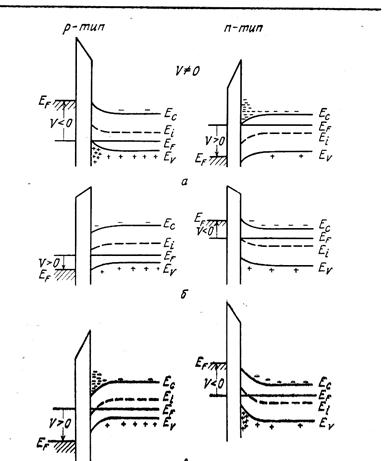
Если к МДП-конденсатору приложить электрическое напряжение, то его обкладки зарядятся. В зависимости от знака и величины приложенного напряжения поверхность полупроводника, будет обогащаться или обедняться основными носителями, или произойдет инверсия проводимости, в том случае, когда концентрация неосновных носителей заряда станет больше чем основных. Энергетические диаграммы, соответствующие различным потенциалам затвора приведены на рис. 2 (потенциал в глубине полупроводника принят равным 0).
Для примера рассмотрим полупроводник p-типа.
При отрицательном потенциале на затворе (Vg<0) к поверхности подтягиваются дырки, и их поверхностная концентрация относительно равновесной возрастает. Это – режим обогащения приповерхностной области полупроводника основными носителями заряда.
При подаче небольших положительных потенциалов на затвор электрическое поле отталкивает дырки от поверхности, и их концентрация вблизи поверхности уменьшается (режим обеднения), но их концентрация все еще превосходит концентрацию электронов, подтянутых электрическим полем к поверхности, так что тип проводимости приповерхностной области остается дырочным, т.е. приповерхностная область обедняется основными носителями заряда относительно объема.
При дальнейшем увеличении потенциала затвора концентрация электронов в приповерхностной области становится больше концентрации дырок в объеме, т.е. происходит изменение (инверсия) типа проводимости.
|
| Рис. 2. Энергетические диаграммы при различных смещениях |
Аналогичные явления будут иметь место для полупроводника n-типа (при этом искривление зон на диаграммах будет направлено в другую сторону).
В общем случае концентрации носителей изменяются по законам:

| (5) |

| (6) |
Здесь 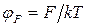 – потенциал уровня Ферми,
– потенциал уровня Ферми,  – потенциал собственного полупроводника (его часто принимают за нулевой), φT = kT/q – тепловой потенциал равный 0,026 В при комнатной температуре. Для p-типа
– потенциал собственного полупроводника (его часто принимают за нулевой), φT = kT/q – тепловой потенциал равный 0,026 В при комнатной температуре. Для p-типа 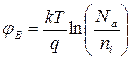 , для n-типа
, для n-типа 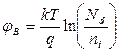 , ni–собственная концентрация носителей.
, ni–собственная концентрация носителей.

|
| Рис. 3. |
Изменение поверхностного заряда индуцирует изменение заряда в объеме полупроводника, что сопровождается изменением изгиба зон вблизи поверхности.
Если величина энергии q∙φ(x) измеряется относительно середины запрещенной зоны (рис. 3), то зная величину потенциала φ(x), возможно рассчитать распределение носителей заряда в приповерхностной области:
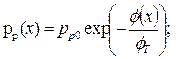
| (7) |
 . .
|
Для характеристики этого изгиба будем использовать понятие поверхностного потенциала φs.
Проведем оценку толщины обедненного слоя для структуры, представленной на рис. 3 в случае обеднения. Пусть полупроводник имеет только акцепторную примесь. Тогда уравнение Пуассона примет вид:
 
| (8) |
Интегрируя с граничными условиями φ=0,  при x=w, получим:
при x=w, получим: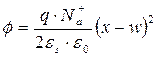 .
.  , отсюда
, отсюда  , таким образом, толщина слоя ОПЗ тем больше, чем больше поверхностный потенциал и чем слабее легирован полупроводник.
, таким образом, толщина слоя ОПЗ тем больше, чем больше поверхностный потенциал и чем слабее легирован полупроводник.
Введем дебаевскую длину дырок  как расстояние, на котором изменение потенциальной энергии носителя заряда равно его тепловой энергии
как расстояние, на котором изменение потенциальной энергии носителя заряда равно его тепловой энергии  .
.