ЛЕКЦИЯ 14

Таблица. Явления переноса в идеальных газах

Общее описание явлений переноса

 

Описанные выше явления переноса имеют много общего с формальной точки зрения. Во-первых, уравнения, выражающие основной закон переноса, формально имеют одинаковый вид. Во-вторых, во всех случаях имеется какая-нибудь переносимая величина, при возникновении градиента некоторых величин. Направление переноса потоков связано с градиентами величин знаком «минус». В. третьих, все рассмотренные явления переноса справедливы при слабом нарушении равновесного состояния системы. Для сравнения явлений переноса в идеальных газах, можно сделать таблицу, в которой в компактной форме видны все различия и сходства рассмотренных явлений переноса.

 

 

Явление	Переносимая величина	Основной закон и уравнение переноса	Коэффициент переноса	Связь между коэффициентами переноса	Зависимость коэффициентов переноса от Т и Р
Диффузия	Количество вещества, или масса, или число молекул	Закон Фика. или			При фиксированной температуре D ~ 1/P, то есть обратно пропорционален давлению. При фиксированном давлении D ~ .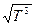
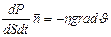
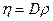
Вязкость	Импульс упорядоченного движения слоёв	Закон Ньютона			η ~ 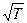, η не зависит от давления
Теплопроводность	Количество теплоты (энергия)	Закон Фурье			χ ~ 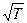, χ не зависит от давления

 

Явления переноса в жидкостях и твёрдых телах формально можно описать с помощью аналогичных уравнений переноса. Однако механизм переноса в них отличается от механизма переноса в идеальных газах и выражения коэффициентов переноса невозможны в том же виде, что и для идеальных газов, поскольку для жидкостей и твёрдых тел, где нельзя пренебречь взаимодействием между молекулами, бессмысленно понятие средней длины свободного пробега.

Кроме формального сходства, следует отметить, что все рассмотренные явления переноса описывают необратимые процессы. Уравнения переноса – это макроскопические уравнения. Используя эти уравнения, можно рассчитать переносимую величину через любую площадь за любой промежуток времени. Покажем это на примере расчёта массы диффундирующего вещества. Из уравнения (5.13) выразим массу, перенесённую через элементарную площадку dS за бесконечно малый промежуток времени dt: 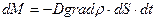. Для нахождения массы ΔМ, перенесённой через площадку S за промежуток времени Δt , необходимо проинтегрировать dM по площади и по времени:

.