Лабораторная работа №11. Изучение вращательного движения твердого тела при помощи маятника Обербека

Цель работы –изучение законов динамики вращательного движения твердого тела, измерение и расчет его момента инерции, а также экспериментальная проверка теоремы Гюйгенса-Штейнера.

Оборудование.В настоящей работе используется установка, входящая в состав системы приборов для лаборатории «Физические основы механики». Общий вид маятника Обербека представлен на рисунке 1.

 

Рис. 1. Установка «Маятник Обербека».

 

На основании (1), закреплен электрический блок (2) и вертикальная колонна (3), на колонне имеются три кронштейна, два из них удерживают фотоэлектрические датчики: это нижний, неподвижный (5) и верхний, подвижный (12). К третьему кронштейну (4) приклеены резиновые амортизаторы для остановки груза. На нижней втулке (8) установлена крестовина и двухступенчатый диск (9), на который наматывается нить. По стержням крестовины могут перемещаться четыре груза одинаковой массы (10), входящие в комплект установки. Нить перекинута через верхний блок (13), а на ее конце привязан постоянный груз (7). На него можно устанавливать дополнительные грузики. В верхней части колонны закреплен электромагнит (14). Время движения измеряется при помощи секундомера, который запускается после прохождения грузом верхнего датчика (11) и останавливается после прохождения через оптический датчик (6). Под действием силы натяжения нити крестовина вращается относительно горизонтальной оси. В момент прохождения грузом нижнего датчика электромагнит (14) останавливает крестовину и диск со шкивом. Тогда на табло электрического секундомера высвечиваются показания времени движения. На колонну нанесена миллиметровая шкала для отсчета пройденного грузом (7) расстояния. Это расстояние можно менять, передвигая верхний оптический датчик. Прибор включается нажатием клавиши «СЕТЬ». После нажатия клавиши «СБРОС» происходит обнуление секундомера; электромагнит (15) фиксирует блок. После нажатия клавиши «ПУСК», становится возможным вращение крестовины.

Теория эксперимента.Рассмотрим вращательное движение Маятника Обербека - крестовины с закрепленными на ней грузами - относительно оси, проходящей через ее центр. Воспользуемся уравнением динамики вращательного движения:

. (1)

Здесь 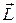– вектор момента импульса, 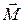- сумма моментов внешних сил, действующих на тело. Такими силами будут сила трения в блоке крестовины и сила упругости нити, на которой подвешен груз m. Вектор момента импульса можно записать в виде произведения момента инерции крестовины J и вектора угловой скорости :

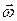. (2)

Тогда уравнение (1) примет вид:

. (3)

На груз m действуют две силы: сила упругости нити и сила тяготения. Ускорение движения груза можно найти, применив второй закон Ньютона:

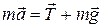. (4)

Рис. 2. Крестовина со шкивом для нити.

 

Уравнение (3), спроецированное на ось вращения, проходящую через ось блока, имеет вид:

. (5)

В уравнении (5) момент внешних сил складывается из момента силы упругости нити T и момента силы трения F_тр в блоке. Абсолютное значение момента силы упругости нити равно T·r. Здесь r – радиус шкива, на который намотана нить. Груз m, подвешенный на нити будет поступательно двигаться с некоторым ускорением. За положительное направление движения выберем направление сверху вниз, тогда уравнение (4) примет вид:

. (6)

Между ускорением поступательного движения груза и угловым ускорением вращательного движения крестовины существует связь, вида:

. (7)

Умножим уравнение (4) на r и учтем уравнение связи (7), получим:

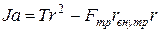. (8)

Из этого уравнения выразим T и подставим в (6), получим:

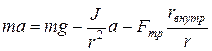. (9)

Если масса груза m мала, то мы не можем пренебрегать силой трения в блоке, и ускорение будет иметь вид:

. (10)

Числитель дроби в формуле (10) не может быть отрицательным (ускорение груза будет всегда направлено вниз), поэтому, если масса m слишком мала, блок не будет вращаться вовсе. Движению будет препятствовать сила трения покоя, принимающая значения в интервале:

, (11)

Здесь m₀ – наименьшая масса груза, при которой блок и крестовина едва начинают вращаться. Если сила трения мала, или 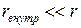, а масса m достаточно велика, то есть значительно превышает m₀, то последним членом в правой части (9) можно пренебречь, тогда формула для ускорения груза m примет вид:

. (12)

Теперь найдем силу упругости нити. Для этого вернемся к формуле (6):

. (13)

Момент этой силы:

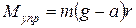. (14)

Если в эксперименте определить ускорение груза, то для того чтобы найти момент силы упругости, остается только взвесить груз и измерить радиус шкива. Будем считать силу трения в уравнении (5) пренебрежимо малой:

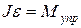, (15)

или . (16)

Момент инерции крестовины можно рассчитать по формуле:

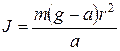. (17)

Ускорение a можно рассчитать, измеряя время t прохождения груза m расстояния h между датчиками:

. (18)

Таким образом, мы можем выразить момент инерции крестовины через экспериментально определяемые величины:

. (19)

С помощью формулы (19) можно рассчитать момент инерции маятника Обербека, измерив в эксперименте величины m, r, h и t. Если передвинуть грузы от оси вращения на крестовине, то момент инерции маятника Обербека изменится. Момент инерции будет складываться из момента инерции втулки с двухступенчатым диском, крестовины J₀ и момента инерции четырех стержней крестовины J_ст, центры масс которых находятся на расстоянии 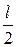от оси вращения:

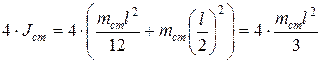, (20)

и, наконец, момента инерции 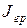четырех грузов , находящихся на расстоянии R от оси:

. (21)

Тогда момент инерции крестовины с грузами можно рассчитать по формуле:

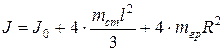. (22)

Согласно теореме Гюйгенса-Штейнера, момент инерции маятника зависит от положения грузов на стержнях. Если в ходе измерений массу m, подвешенную на нити, отставлять постоянной, и менять положение R закрепленных на спицах тел, то ускорение a поступательного движения груза m, согласно формуле (12), а также, связанное с ним по формуле (7) угловое ускорение ε, будут меняться обратно пропорционально моменту инерции креста Обербека. К этому же выводу можно прийти, анализируя формулу (19). Меняя положение R грузов m_гр относительно оси вращения, а, значит и момент инерции J крестовины, и измеряя при этом величины h и t, можно проверить справедливость зависимости формулы для момента инерции (22) от величины R², и, тем самым, выполнить экспериментальную проверку теоремы Гюйгенса-Штейнера.

Если же менять массу груза, подвешенного на нити, то, зная время движения и расстояние, можно рассчитать угловое ускорение вращения блока, пользуясь связью (7), по формуле:

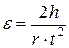, (23)

и опытным путем убедиться в справедливости уравнения динамики вращательного движения (1) и связанного с ним уравнения (5).

В лаборатории механики также имеется лабораторная механическая установка «маятник Обербека» без электронного блока, которая позволяет выполнять аналогичные измерения, но при помощи ручного секундомера.