Критерий устойчивости Найквиста. Формула Найквиста
Дробовый эффект
Дробовым эффектом называется небольшие флуктуации величины электрического тока от среднего значения, вызванные неравномерностью диффузии носителей тока в полупроводниках или неравномерностью эмиссии электронов с катода в электровакуумных приборах.
Дробовой и тепловой шумы – не понижаемые виды шума, возникающие в соответствии с законами физики. Самый дорогой и тщательно изготовленный резистор имеет тот же тепловой шум, что и дешевый углеродный резистор с тем же сопротивлением.
Термин «дробовой эффект» (а также дробовой шум) появился из-за того, что благодаря нему в громкоговорителе, подключённом к выходу усилителя или радиоприёмника, появляется акустический шум, напоминающий шум сыплющихся дробинок.
Формула Найквиста широко используется при расчёте тепловых шумов в измерительных и радиотехнических устройствах. Она определяет величину тепловых флуктуаций тока или напряжения в электрической цепи. Получена формула американским физиком Х. Найквистом в 1928г.
Согласно ней, обусловленное тепловыми флуктуациями среднее значение квадрата напряжения на концах проводника с сопротивлением R, находящегося в состоянии теплового равновесия при абсолютной температуре Т, равно:
 (1).
(1).
При низких температурах и достаточно высоких частотах, когда h kT вместо формулы (1), следует пользоваться более общим выражением:
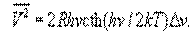 (2).
(2).
Критерий Найквиста был разработан американским физиком Найквистом и опубликован в 1932 году. Он заключается в исследование устойчивости замкнутой системы по заданной амплитудно-фазовой характеристике системы в разомкнутом состоянии. Для этого исследователю необходимо иметь амплитудно-фазовую характеристику (АФХ) разомкнутой системы и информацию о распределении корней характеристического уравнения А(р)=0 разомкнутой системы. Варианты этого распределения обычно классифицируются и сводятся к трем случаям:
1. Разомкнутая система устойчива, то есть все корни полинома А(р) являются левыми.
2. Разомкнутая система неустойчива – полином А(р) имеет к правых корней и предполагается их отсутствие на мнимой оси.
3. Полином А(р) имеет корни на мнимой оси.