Два способа описания природы на макроуровне.

Используя полученные знания на макроуровне в условиях теплового равновесия, можно вполне описать, задав макропараметры, характеризующие как макрообъекты, так и макросостояния. В то же время мы знаем, что каждый макрообъект состоит из известных микрообъектов – атомов, молекул, ядер и электронов. Иными словами, нужно выразить макропараметры через известные характеристики микрообъектов.

Микросостояние обязательно зависит от абсолютной температуры термостата Т, а в более общих случаях от химического потенциала m и давления Р.

В то же время макропараметры, являющиеся характеристиками макрообъектов самих по себе и имеющие аналоги на микроуровне (энергия, число частиц и т.п.), могут быть вычислены по известному микросостоянию в тепловом равновесии. В этом случае соответствующие макропараметры оказываются средними значениями микропараметров по совокупности микрочастиц, составляющих макрообъект., в частности, внутренняя энергия макрообъекта имеет вид

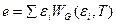(10.7).

где – характерные энергии микрочастиц, a W_G – распределение Гиббса, имеющее смысл вероятности того, что микрочастица входит в состав групп с энергией в условиях теплового равновесия, характеризуемого температурой термостата Т.

Что же касается энтропии, то она может быть вычислена путем усреднения самого распределения Гиббса. После такого усреднения всякая зависимость от характеристик микрочастиц в энтропии исчезает, и она оказывается зависящей от макропараметров, включая макропараметры Т и m, никак не связанные с характеристиками микрочастиц.

Таким образом, из изложенного следует, что в принципе возможны два независимых способа описания природы на макроуровне. В одном из способов описания используются макропараметры, характеризующие макрообъект и его макросостояние в условиях теплового равновесия. Все они равноправны и взаимосвязи между ними определяются уравнением состояния. Изменение энергии макрообъекта в равновесном макропроцессе определяются формулой

(10.8),

называемым основнымтермодинамическимравенством. При этом энтропия S характеризует степень неупорядоченности макрообъекта.

В другом способе описания исходят из универсального микросостояния в тепловом равновесии, называемого распределением Гиббса. Оно зависит от макропараметров, которые в первом способе фиксировали макросостояние, и поэтому они не могут быть вычислены по распределению Гиббса. В то же время макропараметры, относящиеся к макрообъекту, например, энергию e можно вычислить как некие средние значения по распределению Гиббса. При этом то же самое изменение энергии макрообъекта в равновесном макропроцессе, что и выше можно записать в виде

(10.9),

где первый член соответствует передаче теплоты Q, а второй член – работе (-dA).

Контрольные вопросы:

1. Какими особенностями обладает состояние теплового равновесия?

а. При заданных внешних условиях тепловое равновесие единственно.

б. Тепловое равновесие устойчиво.

в. Не зависит от начальных условий, с которых начался переход к тепловому равновесию.

г. Для его задания достаточно фиксировать всего несколько физических величин (макропараметры).

д. Всеми вышеперечисленными.

 

2. В чем различие между детерминированным и стохастическим движениями?

а. Наличие у стохастического движения энтропии.

б. Наличие у детерминированного движения энтропии.

в. Они одинаковы.

 

3. Что такое энтропия?

а. Энтропия – это величина, сохраняющаяся наряду с энергией в равновесных микропроцессах;

б. Энтропия – это величина, сохраняющаяся наряду с энергией в равновесных макропроцессах;

в. Энтропия – это микропроцесс;

г. Энтропия – это величина, сохраняющаяся наряду со скоростью в равновесных микропроцессах.

 

4. Как энтропия изменяется в равновесных процессах?

а. в ходе равновесных макропроцессов не меняется DS_{равновес}=0;

б. в ходе равновесных макропроцессов DS_{равновес}>0;

в. в ходе равновесных макропроцессов DS_{равновес}<0;

г. в ходе равновесных макропроцессов не меняется DS_{равновес}=0.