Исследуем достаточные условия простейшей задачи вариационного исчисления

Содержание

ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ

ПОСОБИЕ

к курсовой работе

для студентов III курса

специальности

"Прикладная математика"

дневного обучения

Москва — 2009

ББК 22.161.5

Е70

Рецензент: к.ф.-м.н., доц. Аль-Натор М.С.

Ерзакова Н.А.

Е70 Вариационное исчисление: Пособие к курсовой работе.- М.: МГТУ ГА, 2009. – 44 с.

Пособие включает правила оформления курсовой работы по вариационному исчислению, а также примерные схемы выполнения всех заданий.

Пособие содержит изложение ключевых моментов курса вариационного исчисления. Приведены примеры задач вариационного исчисления, возникающие в авиации.

В процессе выполнения работы рекомендуется воспользоваться системами компьютерной математики: Mathematica, Maple, MathCAD, MATLAB.

Завершает пособие список основных и дополнительных вопросов к защите курсовой работы.

Данное пособие издается в соответствии с рабочей программой учебной дисциплины ДС.11 "Вариационное исчисление" по Учебному плану для студентов специальности 230401 "Прикладная математика".
Рассмотрено и одобрено на заседаниях кафедры Прикладной математики 20.10.09 (протокол № 2) и методического совета 20.10.09 (протокол № 1).

Редактор

______________________________________________________________________

Подписано в печать

Печать офсетная Формат 60x84 1/16 уч.-изд. л.

…… усл. печ. л. Заказ №. Тираж 300 экз.

____________________________________________________________________

Московский государственный технический университет ГА

125993 Москва, Кронштадский бульвар, д. 20

Редакционно-издательский отдел

125493 Москва, ул. Пулковская, д. 6а

ÓМосковский государственный

технический университет ГА,2007

Задание 1. Задание 2. Задание 3. Задание 4. Задание 5. Задание 6. Задание 7. Приложение Приложение Приложение

Введение……………………………………………………………… Уравнение Эйлера…………………………………………………… Дифференциал Гато…………………………………………………. Условия Лежандра, Якоби, Вейерштрасса, достаточные условия существования экстремума…………………………………………. Функционал энергии………………………………………………… Равносильность задачи вариационного исчисления с задачей нахождения обобщенного решения краевой задачи…………………. Существование и единственность решения системы Ритца……… Нахождение приближенного решения по методу Ритца…………. Заключение…………………………………………………………… Методические указания по оформлению курсовой работы………. Титульный лист……………………………………………………… Основные вопросы к защите курсовой работы……………………. Дополнительные вопросы к защите курсовой работы…………….. Список литературы…………………………………………………

Введение

Изучение задач, связанных с нахождением экстремумов функционалов, составляет содержание вариационного исчисления.

Задачи вариационного исчисления и оптимального управления, тесно связанного с курсом вариационного исчисления, возникают и в авиации. Приведем примеры:

Задача навигации:Как изменится курс движения воздушного судна, если на одном из участков движения оно попадает в зону усиленного потока воздуха?

Задача С. А. Чаплыгина: По какой замкнутой кривой в горизонтальной плоскости должен двигаться центр тяжести самолёта, имеющего собственную скорость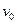, чтобы за время облететь наибольшую площадь, если даны постоянное направление и постоянная величина скорости ветра?

Вариационное исчисление - один из самых старых и наиболее разработанных разделов нелинейного функционального анализа[1].

Однако изначально вариационное исчислениеполучилосамостоятельное развитие,не связанное с функциональным анализом,называемое в дальнейшем наивной теорией вариационного исчисления[2,3,5].

Цель курсовой работы изучить различные подходы к решению вариационных задач на примере простейшей задачи вариационного исчисления.

В заданиях 1 и 3 методами наивной теории вариационного исчисления, т.е. на языкевариацийзаписываетсянеобходимое условие существования экстремума функционалаипроверяются достаточные условия.

Для функционала 1)уравнение Эйлера имеет единственное решение (экстремаль). Для функционала 2) найти точное решение нельзя, так как коэффициенты линейного неоднородного обыкновенного дифференциального уравнения второго порядка не постоянны.

В задании 2 выводится уравнение Эйлера из равенства нулю дифференциала Гато.

Для применения методов функционального анализа, и, в частности, метода Ритца, необходимо изучить пространства Соболева(задание 4) [6,7,8,11,12].

Взадании 5на основании теории дается обоснование того, что экстремаль функционала 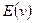в 1), найденная в задании 1, является единственной функцией, доставляющей минимум для функционала 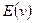в 1).

Здесь же обосновывается равносильность задачи вариационного исчисления с решением задачи Дирихле для эллиптического уравнения .

По методу Ритца находится приближенное решение функционала 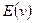в 2)(задания 6,7).

В процессе выполнения работы рекомендуется воспользоваться системами компьютерной математики: Mathematica, Maple, MathCAD, MATLAB [4,9].

Задание 1.Уравнение Эйлера

Найти все экстремали функционала 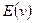, удовлетворяющие указанным граничным условиям в задаче 1); записать уравнение Эйлера в задаче 2).

Выбрать свой вариант.

Вариант 1. 1). .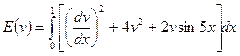

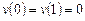2). .

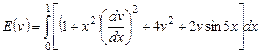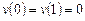Вариант 2. 1), .

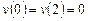2), .

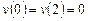Вариант 3. 1), .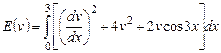

2), .

Вариант 4. 1), .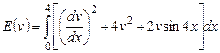

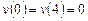2), .

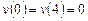Вариант 5. 1), .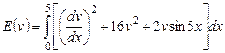

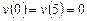2), .

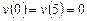Вариант 6. 1), .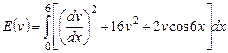

2), .

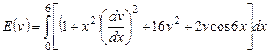Вариант 7. 1), .

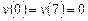2), .

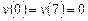Вариант 8. 1), .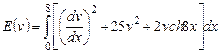

2), .

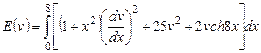Вариант 9. 1), .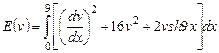

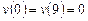2), .

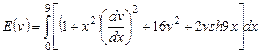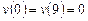Вариант 10. 1), .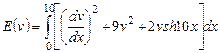

2), .

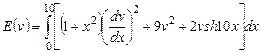Вариант 11. 1), .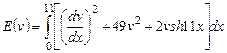

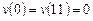2), .

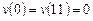Вариант 12. 1), .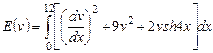

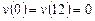2), .

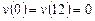Вариант 13. 1), .

2), .

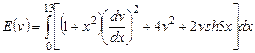Вариант 14. 1), .

2), .

Вариант 15. 1), .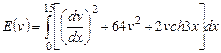

2), .

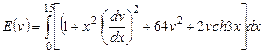Вариант 16. 1), .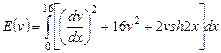

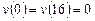2), .

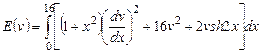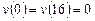Вариант 17. 1), .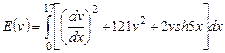

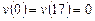2), .

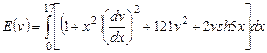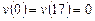Вариант 18. 1), .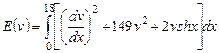

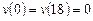2), .

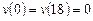Вариант 19. 1), .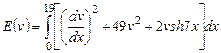

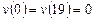2), .

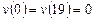Вариант 20. 1), .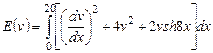

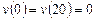2), .

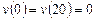Вариант 21. 1), .

2), .

Вариант 22. 1), .

2), .

Вариант 23. 1), .

2), .

Вариант 24. 1), .

2), .

Вариант 25. 1), .

2), .

Вариант 26. 1), .

2), .

Вариант 27. 1), .

2), .

Вариант 28. 1), .

2), .

Вариант 29. 1), .

2), .

Вариант 30. 1), .

2), .

Вариант 31. 1), .

2), .

Вариант 32. 1), .

2), .

Примерная схема выполнения задания 1

Пусть – функция, имеющая непрерывные частные производные до 2-го порядка включительно по всем своим аргументам. Тогда интеграл

(1.1)

являетсяфункционалом , численное значение которого определяется выбором функции на из линейного нормированного пространства.

Пусть функционал определен на множестве . Функции можно рассматривать не только как элементы пространства , но и как элементы . Локальный экстремумфункционала в пространстве называетсясильным, а в пространстве - слабымлокальным экстремумом. Всякий сильный экстремумфункционала является и слабым, а обратное,вообще говоря, неверно.

Простейшая задача вариационного исчисления

Требуется среди всех функций (имеющих непрерывную производную) и удовлетворяющих условиям

, , (1.2)

найти ту функцию, при которой достигается слабый экстремум функционала (1.1).

Для того чтобы функционал (1.1) достигал слабого экстремума на функции , где есть внутренняя точка области определения функционала, необходимо, чтобы эта функция удовлетворяла уравнению Эйлера

. (1.3)

Определение (экстремали). Решения (интегральные кривые) уравнения Эйлера называют экстремалями функционала (1.1).

Пример 1.1. Найти все экстремали функционала

удовлетворяющие граничным условиям .

Решение. В данной простейшей задаче вариационного исчисления (1.1), (1.2) подынтегральная функция , поэтому уравнение Эйлера (1.3) имеет вид . Его общее решение . Из условий получим систему уравнений для определения и :

откуда находим , . Следовательно, в рассматриваемой задаче существует единственная экстремаль .

Задание 2. Дифференциал Гато

Дать теоретическое обоснование того, что уравнение Эйлера является необходимым условием слабого экстремума функционала (1.1).

Записать слабый дифференциал Гато или первую вариацию для функционалов 1), 2) (см. соответствующий вариант) двумя способами.

Примерная схема выполнения задания 2

Определение (дифференциал Гато). Пусть , - два линейных нормированных пространства и - отображение, действующее из некоторого открытого подмножества в . Слабым дифференциалом или дифференциалом Гато отображения в точке (при приращении ) называется предел

где - числовой параметр, а сходимость понимается как сходимость по норме.

Замечание. Слабый дифференциал может и не быть линеен по . Если же такая линейность имеет место, т.е. если

где - ограниченный линейный оператор, то этот оператор называется слабой производной (или производной Гато).

Иногда, следуя Лагранжу, выражение называют первой вариациейотображения . Будем обозначать первую вариацию функционала как .

Теорема 2.1 (необходимое условие экстремума функционала). Необходимым условием достижения функционалом в точке локального экстремума является равенство первой вариации нулю.

Доказательство. Первая вариация - это по определению дифференциал Гато. Поэтому

Если предположить, что , то в сколь угодно малой окрестности нашлись бы точки, в которых разность принимала бы значения разных знаков, что противоречит определению экстремума. Полученное противоречие доказывает утверждение.

Кривые , на которых сравниваются значения функционала, называются допустимыми кривымиили кривыми сравнения.

Обозначимчерез допустимую кривую, на которой функционал достигаетэкстремума, а через произвольную допустимую кривую. Разность называется вариацией кривой.

Вариация есть функция и принадлежит тому же функциональному пространству, что и функция . Поэтому, если , то вариацию можно дифференцировать, причем

,…,,…,.(2.1)

Используя вариацию , можно представить любую допустимую кривую в виде

Рассмотрим семейство кривых

. (2.2)

В выражении (2.2) - фиксированная функция, а - числовой параметр. Очевидно, что при справедливо .

Теорема 2.2 (необходимое условие экстремума функционала (1.1) в простейшей вариационной задаче (1.1), (1.2)).

Необходимым условием экстремума функционала (1.1) в простейшей вариационной задаче (1.1), (1.2) является равенство

Доказательство. Если рассматривать значения функционала (1.1) только на кривых семейства , то функционал превращается в функцию числового параметра :

. (2.3)

Так как - кривая, на которойфункционал (1.1) достигаетэкстремума, то функция достигает своего экстремума при в силу (2.2) и (2.3).

Необходимым условием экстремума функции при является:

. (2.4)

Запишем в развернутом виде (2.3)

откуда следует, что

Принимая во внимание (2.1) и равенства

получим

;

Поскольку , интегрируя второе слагаемое по частям, получим .

Но , в силу определения допустимых кривых. Следовательно, условие (2.4) влечет равенство

справедливое для любого значения . 

Замечание. Слабый дифференциал Гато функционала (1.1) в простейшей вариационной задаче (1.1), (1.2) имеет вид

. (2.5)

Основная лемма вариационного исчисления.Если для каждой непрерывной функции имеем, где функция непрерывна на отрезке , то .

Замечание. Утверждение леммы и ее доказательство не изменяются, если на функцию наложить следующие ограничения: ; имеет непрерывные производные до порядка , ().

Доказательство. Предположив, что в точке , лежащей на отрезке , ,придем к противоречию. Действительно, из непрерывности следует, что если, то сохраняет знак в некоторой -окрестности, , точки . Выберем функцию также сохраняющую знак в этой окрестности и равную нулю вне этой окрестности, получим

Итак, мы пришли к противоречию, следовательно, .

Следствие. Из основной леммы вариационного исчисления и теоремы 2.2 необходимым условием экстремума функционала (1.1) является уравнение Эйлера (1.3).

Пример 2.1. Найти первую вариацию функционала

Решение. Первый способ. Запишем приращение функционала .

Поскольку в выражении - фиксированная функция,

По определению

поэтому

Второй способ. Воспользуемся формулой (2.5) . Так как в данном случае , то =2y и .

Пример 2.2. Найти первую вариацию функционала

(- постоянная).

Решение. Первый способ. Запишем приращение функционала

Имеем .

Поскольку в выражении - фиксированная функция,

По определению

так как

и .

Второй способ. Воспользуемся формулой (2.5) . Так как в данном случае , то .

Задание 3. Условия Лежандра, Якоби, Вейерштрасса, достаточные условия существования экстремума

Проверить условия Лежандра, Якоби, Вейерштрасса, достаточные условия существования экстремума в задаче 1).

Примерная схема выполнения задания 3

, . (3.1)

Замечание. Задачу на максимум можно свести к задаче на минимум, рассмотрев . Поэтому ограничимся рассмотрением задачи на минимум.

Рассуждения на языке вариаций относится к так называемой наивной теории вариационного исчисления, которая имела самостоятельное развитие.

Из теоремы 2.1 следует, что уравнение Эйлера (1.2)

является необходимым условием экстремума.

Если использовать в качестве достаточного условия экстремума дифференциал Фреше второго порядка , то - сильно положительный квадратичный функционал в случае минимума. Однако на практике это редко выполняется.

Поэтому имеет смысл искать достаточные условия второго порядка, отличные от дифференциала Фреше второго порядка.

Так как

то развернутая запись формулы Эйлера следующая:

. (3.2)

Определение (условия Лежандра). Условия Лежандра имеют вид

или .

Усиленные условия Лежандра имеют вид

или .

Замечание. При выполнении усиленного условия Лежандра можно делением свести уравнение (3.2) к обыкновенному дифференциальному уравнению второго порядка

. (3.3)

Поэтому экстремали – это решения краевой задачи (3.3), (3.1).

Уравнение Эйлера, определяющее экстремали, зависит лишь от и не меняется при изменении краевых условий.

Определение (собственного поля экстремалей). Поле экстремалей в области на плоскости называется собственным, если через каждую точку проходит единственное решение уравнения Эйлера.

Определение (центрального поля экстремалей). Поле экстремалей в области на плоскости называется центральным, если все экстремали выходят из одной точки и однократно накрывают .

Для формулировки достаточных условий экстремума, в частности, используется условие Якоби,которое выполняется, если уравнение Якоби

, (3.4)

где , , - соответствующие производные подынтегральной функции, вычисленные на экстремали , удовлетворяющей уравнению Эйлера и граничным условиям, имеет нетривиальное решение , которое:

а) удовлетворяет условию ;

б) не обращается в нуль ни при каких значениях .

Замечание. Нули , отличные от , называются сопряженными точками (точке ). Условие Якоби является условием включения экстремали в центральное поле экстремалей с центром в точке .

Пусть - экстремаль или кривая в функционала , - другая кривая в . Для оценки разности рассматривается интеграл как криволинейный интеграл, т.е. подыскиваются такие функции , , что не зависит от пути интегрирования.

Задачу решает так называемый инвариантный интеграл Гильберта:

, (3.5)

где обозначает геодезический наклон – производную той экстремали в точке , которая проходит через точку .

Обоснование независимости интеграла (3.5) от пути интегрирования может иметь два направления, либо интуитивный поиск функции , такой, что , либо сразу полагают

и проверяют равенство перекрестных производных, т.е.

Последнее гарантирует, собственно, существование подходящей функции , равно как и независимость интеграла (3.5) от пути интегрирования.

Это позволяет оценить разность как интеграл

, (3.6)

взятый вдоль произвольной кривой .

Для достижения минимума достаточно, чтобы подынтегральное выражение в (3.6) было неотрицательно, что представляет собой условие Вейерштрасса

. (3.7)

Напомним, что если функционал определен на множестве и неравенство выполнено при всех и не выполнено при всех то доставляет функционалу слабый локальный минимум.

Если неравенство выполнено при всех то доставляет функционалу сильный локальный минимум.

Теорема 3.1 (достаточные условия слабого минимума). Если на экстремали , удовлетворяющей уравнению Эйлера и граничным условиям, выполняются:

а) условие Якоби;

б) либо условие Вейерштрасса для точек , близких к точкам на экстремали , и для близких к , либо усиленное условие Лежандрана экстремали , то на достигается слабый минимум.

Теорема 3.2 (достаточные условия сильного минимума). Если на экстремали , удовлетворяющей уравнению Эйлера и граничным условиям, выполняются:

а) условие Якоби;

б) либо условие Вейерштрасса для точек , близких к точкам на экстремали , и для произвольных , либо условие Лежандра для точек , близких к точкам на исследуемой экстремали , и для произвольных значениях ,то на достигается сильный минимум.

Пример 3.1. Найти экстремум функционала

, , .

Решение. Найдем экстремаль , удовлетворяющую уравнению Эйлера и граничным условиям. Так как подынтегральная функция не зависит от и явно, то уравнение Эйлера имеет общее решение . Из граничных условий , , находим , . В результате получаем экстремаль .

Проверим достаточные условия сильного минимума:

а) для проверки условия Якоби составим уравнение Якоби. Так как на экстремали производная равна и , , , то уравнение (3.4) имеет вид . Отсюда . Из условия следует и . Так как нетривиальное решение уравнения Якоби при , то условие Якоби выполняется;

б) так как функция трижды дифференцируема по , то применим условие Лежандра. Поскольку не сохраняет знака при любых , то достаточные условия сильного минимума не выполнены. Вопрос о наличии сильного минимума остается открытым.

Проверим достаточные условия слабого минимума:

а) условие Якоби выполняется;

б) применим усиленное условие Лежандра. Поскольку на экстремали , то достаточные условия слабого минимума выполнены. Экстремаль доставляет слабый минимум функционалу.

Проверим условие Вейерштрасса. Функция

может иметь любой знак, если принимает произвольные значения. По замечанию [3, c.119] условие Вейерштрасса является необходимым условием, следовательно, сильный минимум на прямой не достигается. На данной экстремали . Поэтому , если принимает значения, близкие к , что еще раз подтверждает выполнение достаточных условий слабого минимума.

Пример 3.2. Пусть для функционала

(- постоянная)

на экстремали , удовлетворяющей уравнению Эйлера и граничным условиям, выполняется условие Якоби. Проверить выполнение условия Вейерштрасса.

Решение. В силу (3.7) найдем

В данном случае

Заметим, что не зависимо от и . Поэтому условие Вейерштрасса выполняется для точек , близких к точкам на экстремали , и для произвольных .

По теореме 3.2 для экстремали выполнены достаточные условия сильного минимума. Необходимость в проверке достаточных условий слабого минимума отпадает, поскольку всякий сильный экстремумфункционала является и слабым. 

Задание 4. Функционал энергии

Рассматривая функционал 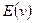в 1) (см. задание 1) как частный случай функционала энергии

, (4.1)

а) проверить выполнение условий , , , ,

б) найти в области регулярное (классическое) решение эллиптического уравнения

, (4.2)

удовлетворяющее граничному условию

, (4.3)

в) найти обобщенное решениекраевой задачи (4.2), (4.3), принадлежащее пространству Соболева .

Примерная схема выполнения задания 4

Определение (пространства Соболева). Множество всех функций из для области , имеющих обобщенные производные до -ого порядка включительно из , называется пространством С.Л.Соболева .

Замечание. Пространства при с нормой

являются банаховыми пространствами.

В частности, если , то

где - это квадрат модуля градиента в точке .

Если , , то

Определение (гильбертова пространства Соболева). Пространство Соболева при (обозначаемое через ) - это гильбертово пространство, в котором скалярное произведение определяется следующим образом:

для любых . Соответственно норма в определяется равенством

Определение(вложения). Пусть и - два нормированных пространства с нормой и , соответственно. Пространство вложено в , если каждый элемент из является элементом из и, кроме того, существует число , такое что