Колебания гармонического осциллятора

Методы и приборы для измерения времени

Время и его измерение

Время как физическая величина, измеряемая в процессах контроля или диагностирования, выступает либо в виде фиксируемого момента, соответствующего некоторому событию, либо в виде интервала времени между событиями.

Количественной оценкой в первом случае служит дата времени, а во втором – интервал времени.

В настоящее время параллельно существуют две системы измерения времени: астрономическая система измерения времени, и атомная система измерения времени, которые дополняют друг друга.

Мера времени это средство измерения времени, предназначенное для воспроизведения интервалов времени заданной длительности или заданных моментов времени.

Приборы и устройства времени по функциональным свойствам разделяются на следующие группы:

а) измерители текущего времени, которые позволяют устанавливать час, минуту, секунду;

б) измерители интервалов времени (секундомеры, реле времени и т.д.);

в) измерители временных физических характеристик (тахометры, счетчики оборотов и др.);

с) программно-временные датчики интервалов времени (таймеры);

д) датчики равномерной скорости (стабилизаторы частоты вращения двигателей, часовые механизмы самопишущих приборов и др.).

Основные элементы любого измерителя времени это источник энергии, колебательная система (осциллятор), счетчик, выходное устройство.

Процедура измерения времени сводится к счету строго периодической последовательности импульсов, формируемых с помощью колебаний осциллятора.

 

Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида

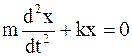или 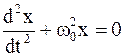. (5.1)

Колебания гармонического осциллятора являются примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики.

Разновидностью одномерного линейного гармонического осциллятора является маятник, без которого невозможна работа механических часов. Использование маятника в часах основано на свойстве изохронности, т.е. не зависимости периода колебаний от величины амплитуды.

В качестве примеров гармонических осцилляторов рассмотрим гармонические колебания систем, называемых физическим и математическим маятниками.

 

4.2.2. Физический и математический маятники

Физический маятник - твердое тело, способное совершать гармоническое колебательное движение относительно оси, на которой оно подвешено. При этом ось не проходит через центр тяжести.

Положение физического маятника в каждый момент времени можно характеризовать углом отклонения от положения равновесия φ. Угол φ играет роль обобщенной координаты.

В поле сил тяготения колебания физического маятника (рис. 5.2) происходят под действие возвращающей силы, составляющей силы тяготения F_t = mg, которую можно разложить на две составляющие: по направлению прямой, перпендикулярной осиF_n, и по направлению, перпендикулярному данному – F_τ. Составляющая F_n не создает вращающего момента, так как она перпендикулярна оси вращения (колебания). Поэтому возвращающей силой, создающей вращающий момент в данном случае, является

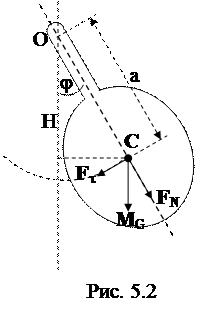F_τ = - mg×sinj, (5.2)

где j - угол отклонения физического маятника от положения равновесия.

При малых углах отклонения (j®0) sinj ®j, следовательно, F_τ= - mgj, а момент этой силы

M = - mgja, (5.3)

где a - расстояние от точки приложения силы до оси вращения.

Согласно основному уравнению динамики вращательного движения, этот вращающий момент M численно равен:

M = Iε. (5.4)

Таким образом, имеем

Iε == - mgja; Iε + mgja = 0;

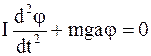. (5.5)

Полученное соотношение является уравнением движения физического маятника. С точки зрения математики, оно однородное, дифференциальное, второго порядка, решение которого имеет вид

j = j₀×sin(ω₀t + α), (5.6)

где α - начальная фаза колебаний.

Решая дифференциальное уравнение, можно определить круговую (циклическую) частоту и период колебаний физического маятника

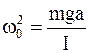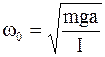; ; (5.7)

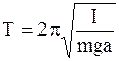. (5.8)

Математический маятник - тело массой m, подвешенное на невесомой, нерастяжимой нити, размерами которого можно пренебречь 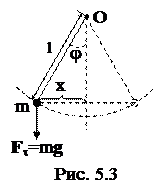(рис.5.3).

Математический маятник совершает гармонические колебания под действием силы тяжести, подобно физическому маятнику.

В этом случае математический маятник можно рассматривать как материальную точку, для которой момент инерции

I = ml², (5.9)

где l - длина математического маятника.

Так как математический маятник - частный случай физического маятника, вся масса которого сосредоточена в одной точке - центре масс, то, подставив в (5.8) значение (5.9) для циклической частоты и периода колебаний математического маятника, получим

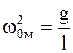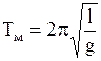;. (5.10)

Из выражений (5.10) видно, что циклическая частота и период колебаний математического маятника зависит от его длины и ускорения свободного падения в данном месте пространства.

Надо отметить, что все рассмотренное справедливо для малых углов отклонения соответствующей системы от положения равновесия. Если данное условие не выполняется, то определение циклических частот и периодов колебаний представляется довольно трудной задачей, так как в этом случае они функционально оказываются зависимыми от угла отклонения:

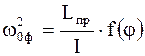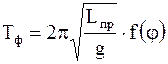;; (5.11)

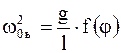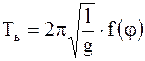;. (5.12)

Примером использования колебаний гармонического осциллятора в устройствах измерения времени является колебательный контур (рис. 5.4).

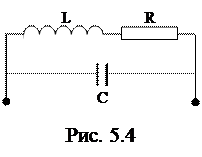Если в таком контуре ток периодически изменяется с течением времени 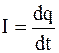, то в контуре возникают электромагнитные колебания.

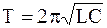. (5.17)

Из выражения (5.17) видно, что период электромагнитных колебаний также не зависит от амплитуды q₀. Колебательный контур используется во многих измерительных системах в качестве генератора колебаний.