Показатели концентрации и централизации

 

Одна из задач статистического анализа структуры заключается и определении степени концентрации изучаемого признака по единицам совокупности или в оценке неравномерности его распределения. Такая неравномерность может иметь место в распределении доходов по груп­пам населения, жилой площади по группам семей, прибыли по группам предприятий и т.д. При исследовании неравномерности распределения изучаемого признака по территории понятие «концентрация» обычно заменяется понятием «локализация».

Оценка степени концентрации наиболее часто осуществляется по кривой концентрации (Лоренца) и рассчитываемым на ее основе ха­рактеристикам. Для этого необходимо иметь частотное распределение единиц исследуемой совокупности и взаимосвязанное с ним частотное распределение изучаемого признака. Для удобства вычислений и повы­шения аналитичности данных единицы совокупности, как правило, раз­биваются на равные группы - 10 групп по 10% единиц в каждой, 5 групп по 20% единиц и так далее.

Наиболее известным показателем концентрации является коэффициент Джини, обычно используемый как мера дифференциации или социального расслоения:

 

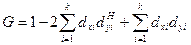(11.10.)

 

где 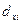- доля i-ой группы в общем объеме совокупности;

- доля i-ой группы в общем объеме признака;

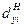- накопленная доля i-ой группы в общем объеме признака.

Если доли выражены в процентах, данную формулу можно преобразовать:

для 10%-го распределения –

(11.11.)

для 20%-го распределения –

(11.12.)

Чем ближе к 1 (100%) значение данного признака, тем выше уровень концентрации; при нуле мы имеет равномерное распределение признака по всем единицам совокупности.

Оценка степени концентрации также может быть получена на основе коэффициента Лоренца:

 

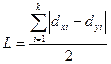(11.13.)

 

При использовании данного коэффициента можно оперировать как долями единицы, так и процентами. Коэффициент Лоренца изменяется в тех же границах, что и коэффициент Джини.

Определим степень концентрации доходов населения по данным таблицы 11.4.:

 

Таблица 11.4.