Аналитический метод анализа переходных процессов в комбинационных ДУ

 

При рассмотрении переходных процессов в бесконтактных ДУ мы установили следующее.

В дискретных устройствах, функциональная схема которых построена в соответствии с дизъюнктивной нормальной формой функции, возможно появление состязаний сигналов только типа риск в единице. Эти состязания могут привести к нарушению работы ДУ при изменении состязующегося сигнала x_i с 1 на 0.

В дискретных устройствах, функциональная схема которых построена в соответствии с КНФ функции, возможно появление состязаний сигналов только типа риск в нуле. Эти состязания могут привести к нарушению работы ДУ при изменении состязующегося сигнала x_i с 0 на 1.

Целью решения задачи анализа переходных процессов является определение и построение функции риска, которая описывает все возможные ситуации появления ложных сигналов на выходе дискретного устройства.

Анализ переходных процессов в комбинационных ДУ может быть выполнен или с помощью карт Карно (при числе входов не более 5-6), или аналитическим методом.

Рассмотрим более подробно аналитический метод. В основу аналитического метода положены дизъюнктивное и конъюнктивное разложения логической функции по переменной x_i:

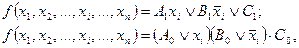
где A, B, C – логические функции, зависящие от остальных переменных.

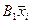Из формулы дизъюнктивного разложения следует, что A₁x_i, C₁ являются импликантами функции f(x). Выражение A₁x_i – есть импликанта функции f(x), принимающая единичные значения на наборах, где x_i = 1. Выражение – есть импликанта функции f(x), принимающая единичные значения на наборах, где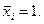

Таким образом, для функции f(x) выражение A₁x_i описывает пути формирования единичного значения выхода, когда x_i = 1. Выражение 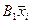описывает пути формирования единичного значения выхода, когда 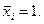Выражение C₁ описывает пути формирования единичного выходного сигнала автомата, не зависящие от x_i.

Состязания сигналов типа риск в единице возникают в автомате при последовательном поступлении соседних единичных наборов (т.е. таких, на которых значения выходов должны быть равны единице), а единичные выходные сигналы формируются различными путями, и других цепей формирования выходного сигнала на этих наборах нет.

Очевидно, что условия для появления состязаний сигналов типа риск в 1 по переменной x_i могут возникать только на тех наборах, когда одновременно обратятся в единицу функции A₁, B₁ и обратится в нуль функция C₁. Отсюда следует, что для ДУ, описываемого ДНФ функции f(x), функция риск в 1 по переменной x_i имеет вид:

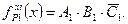
Если работа описывается конъюнктивным разложением функции f(x), то, рассуждая аналогично (для нулевых входных наборов и нулевого значения выхода), делаем вывод, что условия появления состязаний типа риск в 0 по переменной x_i могут возникнуть только на тех наборах, когда одновременно обратятся в нуль функции A₀, B₀ и обратится в единицу функция C₀.

Отсюда следует, что для ДУ описываемого КНФ функции f(x), функция риск в 0 по переменной x_i имеет вид:

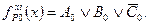
Методика определения функций риска аналитическим методом следующая.

1. По схеме ДУ составляются логические функции, описывающие его функционирование по каждому выходу, и определяются переменные (входные сигналы), по которым возможны состязания – они входят в функции выходов как в прямом (x_i), так и в инверсном 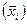виде.

2. По каждой состязующейся переменной функция выхода преобразуется к ДНФ (дизъюнктивное разложение), если выходным элементом является дизъюнктор (И-НЕ), или КНФ (конъюнктивное разложение), если выходным элементом является конъюнктор (ИЛИ-НЕ), и определяются функции A₁, B₁, C₁, A₀, B₀, C₀.

3. С учетом выражений для A₁, B₁, C₁, A₀, B₀, C₀, полученных в п.2, определяются функции риска по переменным x_i –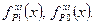

4. Определяются функции риска для ДУ в целом по формулам:

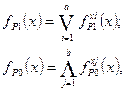
где a(b) – множество переменных, на которых возможны состязания сигналов типа риск в 1 (риск в 0).

Если в результате вычислений окажется, что 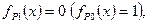то, следовательно, в ДУ отсутствуют состязания сигналов типа риск в 1 (риск в 0).

Методику анализа переходных процессов в комбинационных ДУ аналитическим методом рассмотрим на примерах.

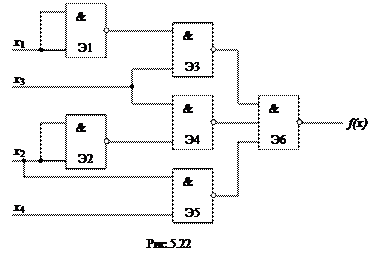
Пример 5.4 Провести анализ переходных процессов в ДУ, функциональная схема которого приведена на рисунке 5.22. Схема построена на шести логических элементах И-НЕ, имеет 4 входа – x₁, x₂, x₃, x₄. Поскольку схема построена на БЛЭ И-НЕ, ее функция выхода легко приводится к ДНФ:

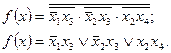
Видим, что схема анализируемого ДУ построена в соответствии в ДНФ функции f(x) и переменная (входной сигнал) x₂ входит в нее как в прямом (x₂), так и в инверсном () виде.

Рисунок 5.22

Значит, в данном автомате возможны состязания по сигналу x₂ типа риск в 1 при изменении его значения с 1 на 0.

Определим функции A₁, B₁, C₁ по переменной x₂:

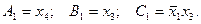
Определим функцию риска в 1 по переменной x₂:

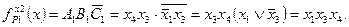
Так как состязания в схеме возможны лишь по переменной x₂, то общая формула риска в единице совпадает с формулой риска в единице по переменной x₂:

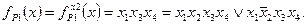
Итак, логическая формула, описывающая риск в единице в рассматриваемом ДУ, имеет вид (в СДНФ):

или в символическом виде при базе x₁x₂x₃x₄:

Полученный результат говорит о том, что в рассматриваемом ДУ на единичных наборах функции риска 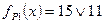выход дискретного устройства равен 1 (есть сигнал), но при переходе от набора 15 к набору 11 в результате изменения переменной x₂ с 1 на 0 наблюдается кратковременное исчезновение сигнала на выходе.

При переходе от набора 11 к набору 15 исчезновения сигнала не происходит, так как переменная x₂ изменяет свое состояние с 0 на 1, а при этом, как нам известно, риска в 1 не возникает.

Рассмотрим рисунок 5.22. При входном наборе 15 (1111) выходы элементов равны соответственно:

Э1 – 0, Э2 – 0, Э3 – 1, Э4 – 1, Э5 – 0, Э6 – 1.

Единичный сигнал на выходе ДУ (Э6) обеспечивается нулевым сигналом на выходе элемента Э5, потому что выходы элементов Э3 и Э4 равны 1.

При входном наборе 11 (1011) выходы элементов равны соответственно:

Э1 – 0, Э2 – 1, Э3 – 1, Э4 – 0, Э5 – 1, Э6 – 1.

Единичный сигнал на выходе ДУ (Э6) обеспечивается нулевым сигналом Э4, так как выходы элементов Э3 и Э5 равны 1.

Однако при переходе от набора 15 к набору 11 переменная x₂ меняет свое значение с 1 на 0, тогда элемент Э5 сработает раньше (изменит свое состояние), чем два элемента Э2 и Э4 в сумме. Поэтому в схеме ДУ возникает такое состояние, когда на время после изменения входов, равное (t_ЗЭ2 + t_ЗЭ4) – t_ЗЭ5, где t_З – время задержки, на входах элементах Э6 все входные сигналы будут равны 1, а следовательно, сигнал на выходе ДУ на это время будет равен 0, т.е. произойдет кратковременное исчезновение сигнала на выходе.

Аналогично можно убедиться, что при переходе от набора 11 к набору 15 исчезновения сигнала на выходе не будет.

Таким образом, в результате исследования переходных процессов в схеме ДУ можно сделать вывод: если при работе данного устройства имеется переход от набора 15 к набору 11, то следует принять меры для устранения состязаний сигналов.

Пример 5.5 Функциональная схема ДУ показана на рисунке 5.23.

Рисунок 5.23

Логическое выражение, описывающее условия его работы, имеет вид:

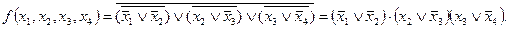
Очевидно, что в рассматриваемом ДУ могут иметь место состязания типа риск в нуле (форма КНФ) по переменным x₂ и x₃, т.е. при таких изменениях состояний входов, при которых x₂ или x₃ меняются с 0 на 1, на выходе ДУ может кратковременно появиться ошибочный единичный сигнал.

Из КНФ получаем:

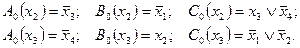
Вычисляем функции риска в нуле по x₂ и x₃:

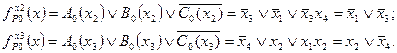
Вычисляем функцию риска в нуле для всего ДУ:

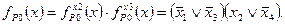
Приведем функцию 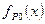к символической форме при базе x₁x₂x₃x₄:

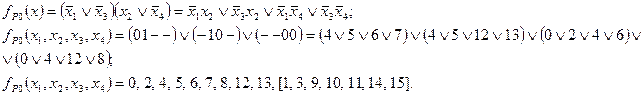Так как риск в нуле проявляется лишь при отсутствии выходного сигнала (сигнал на выходе равен 0), то нас интересуют запрещенные наборы функции 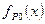, именно на них возможны состязания типа риск в нуле.

Этот же результат может быть получен, если определить инверсную функцию 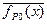и найти ее рабочие ВС. Именно они и будут запрещенными наборами для функции .

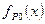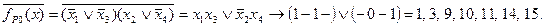
Полученный результат говорит о том, что на входных наборах 1, 3, 9, 10, 11, 14, 15 (при базе x₁x₂x₃x₄) на выходе ДУ сигнала быть не должно (нулевой сигнал). Однако вследствие наличия состязаний типа риск в нуле по переменной x₂ и x₃ при переходах входных сигналов 10 → 14, 11 → 15, 1 → 3, 9 → 11, когда переменные x₂ и x₃ изменяют свои значения с 0 на 1, возможны появления на выходе кратковременных ложных единичных сигналов.