Бесконтактных элементах

Анализ комбинационных дискретных устройств, построенных на

 

Анализ комбинационных дискретных устройств, построенных на бесконтактных элементах, проводится в соответствии с методикой, изложенной в 4.1.

Отметим, что наиболее просто получить первоначально модель автомата можно в виде логических формул. При этом удобно анализ проводить от выходов ко входам. В этом случае этап 4 методики анализа, изложенной в 4.1, следует проводить в таком порядке.

Обозначаются промежуточными переменными выходов всех внутренних логических элементов. К внутренним элементам относятся все элементы, кроме выходных, с которых снимаются выходные сигналы

z1, z2, …, zm.

Определяются логические формулы, описывающие значения сигналов на каждом выходе дискретного устройства с учетом введенных промежуточных переменных и функций, реализуемых логическими элементами.

Определяются логические формулы, описывающие значения сигналов (промежуточные переменные) на выходах внутренних элементов с учетом логических функций, реализуемых этими элементами.

Путем последовательной подстановки в формулы, полученные по п.2, значений промежуточных переменных, полученных по п.3, до полного их исключения, определяются логические формулы, описывающие функционирование заданного дискретного устройства.

Полученные логические формулы, связывающие входные и выходные сигналы, приводятся к ДНФ, а затем к СДНФ и, если нужно, строится таблица состояний (соответствия) и получается символическая форма условий функционирования ДУ.

Изложенную методику рассмотрим на примерах.

Пример 4.1 Получить условия работы комбинационного автомата, изображенного на рисунке 4.1, в виде логических формул, таблицы состояний и символической формы.

По функциональной схеме (см. рисунок 4.1) определяем, что дискретное устройство построено на бесконтактных логических элементах, входами являются «Вход 1», «Вход 2», «Вход 3», «Вход 4», а выходами – «Выход 1», «Выход 2», «Выход 3», которые обозначим x1, x2, x3, x4 и z1, z2, z3 соответственно.

Изучение логических элементов D1-D10, на которых реализован автомат, показывает следующее.

Элементы D1, D2, D3, D8 и D9 производят формирование, усиление или повторение сигнала. Это устанавливается по символу функции, который помещен в основном поле условного обозначения этих элементов. Следовательно, эти элементы выполняют логическую функцию повторения, являются вспомогательными и при анализе могут быть исключены. Другие элементы схемы автомата – D4, D5, D6, D7, D10, как можно судить по символам функций, выполняют логические функции И-ИЛИ-НЕ (D4), НЕ (D5, D10), И (D6), ЗАПРЕТ-НЕ (D7). Исключим из анализа вспомогательные элементы D1, D2, D3, D8 и D9; выходы внутренних элементов D4, D5, D7 обозначим буквами (промежуточными переменными) a1, a2, a3 и построим упрощенную функциональную схему (Рисунок 4.2).

Для несложных комбинационных автоматов упрощенная функциональная схема может не строится, а соответствующие исключения и обозначения делаются непосредственно на функциональной схеме.

По упрощенной функциональной схеме (Рисунок 4.2) запишем логические формулы, описывающие сигналы на выходах:

Определим логические формулы, описывающие сигналы на выходах внутренних элементов D4, D5, D7:

 
 
Рисунок 4.1

 

 
 

 
 
Рисунок 4.2
 
 


Последовательно подставляя в выражение для z1, z2, z3 значения a1, a2, a3 и произведя преобразования, получим условия работы ДУ в ДНФ:

 

Приводим условия работы ДУ к СДНФ методом домножения на недостающую переменную:

Проведя необходимые преобразования, получим:

 

Условия работы ДУ приводить к СДНФ лучше через ОК. Так, например, для перейдем к ОК и затем к наборам при базе x1 ÷ x4

Теперь переходим к СДНФ:

Строим таблицу состояний на 4 входных сигнала и 3 выхода. Выбираем базу x1x2x3x4, т.е. присваиваем входам x1, x2, x3, x4 веса 23, 22, 21, 20. Таблица состояний представлена в виде табл.4.1.

Из таблицы состояний очевидны рабочие и запрещенные весовые состояния (наборы) для каждого выхода. Поэтому непосредственно из таблицы получаем символическую форму записи условий работы ДУ:

При решении инженерных задач анализа комбинационных ДУ, как правило, СДНФ и таблицы состояний не получают, а от ДНФ условий работы сразу переходят к символьной форме записи, используя метод обобщенных кодов (решетки соседних чисел).

Выберем базу x1, x2, x3, x4 и по полученным ДНФ запишем условия работы для каждого выхода в обобщенных кодах:

По решетке соседних чисел или перебором вместо «–» 0 и 1 получим рабочие числа. Проведя упрощения по закону повторения, получим символическую форму условий работы ДУ в сокращенном виде – только рабочие весовые состояния. Остальные (до полного перебора от 0 до 15) являются запрещенными.

 

 

Таблица 4.1


Входные сигналы Выходные сигналы ВС
23 22 21 20
x1 x2 x3 x4 z1 z2 z3

Пример 4.2 Определить условия работы бесконтактного ДУ (Рисунок 4.3), являющегося частью блока 15Я89-1.

Рисунок 4.3
 
 

Заданная функциональная схема является весьма простой, вспомогательных элементов не содержит, поэтому упрощенной схемы строить не нужно. Не нужны также промежуточные переменные.

Запишем последовательно по схеме условия прохождения сигналов. В результате получим функцию, которую реализует данное БДУ:

Перейдем к символической форме при базе a, b, c с использованием решетки соседних чисел:

Анализ закончен. Полученный результат говорит о том, что сигнал (1) на выходе появляется в следующих случаях:

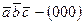– отсутствие на входах сигналов a, b, c (выход );

– присутствие на входе сигнала c (выход );

– присутствие на входах сигналов b, c (выход );

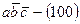– присутствие на входе сигнала a (выход );

Именно так и работает устройство в блоке 15Я89-1.