Взаимное положение точки и прямой
ВЗАИМОПРИНАДлЕЖНОСТЬ ТОЧКИ, ПРЯМОЙ И ПЛОСКОСТИ
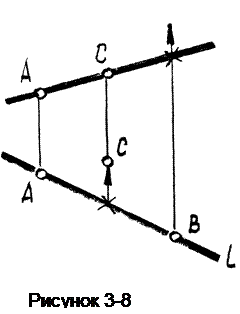 Относительно прямой общего положения l(рисунок 3-8) построим следующие точки:
Относительно прямой общего положения l(рисунок 3-8) построим следующие точки:
1. точка А принадлежитl (АÎl). Задача решается на основании свойства принадлежности;
2. точка В над прямой.
Как построить точку на прямой мы теперь знаем, а поскольку она должна быть над прямой, т, е. выше нее, необходимо внести соответствующее изменение в положение точки на виде спереди;
3. точка С за прямой.
Аналогично предыдущей задаче приходим к выводу, что запрямой означает дальше нее, чему соответствует изменение положения точки на виде сверху.