Круговые сечения поверхностей второго порядка
Теорема о двойном прикосновении позволяет весьма просто строить круговые сечения тех поверхностей второго порядка, которые их имеют.
Для построения круговых сечений надо провести сферу, имеющую двойное прикосновение с данной поверхностью. В этом случае
линия пересечения поверхностей распадается на две плоские кривые, а так как эти линии принадлежат сфере, то они будут являться окружностями.
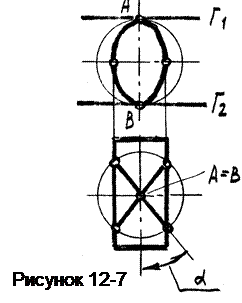 Пример 3. Построить круговые сечения эллиптического цилиндра (рисунок 12-7).
Пример 3. Построить круговые сечения эллиптического цилиндра (рисунок 12-7).
Из произвольной точки оси цилиндра описываем сферу такого радиуса, чтобы она касалась двух образующих цилиндра (см. вид спереди) и пересекала его (см. вид сверху).
Точки А и В будут точками двойного прикосновения, т.к. в них можно провести общие касательные плоскости Г¹ и Г² к цилиндру и сфере.
Линия пересечения сферы с эллиптическим цилиндром будет состоять из двух плоских кривых - окружностей.
Пример 4. Построить круговые сечения эллиптического конуса
(рисунок 12-8).
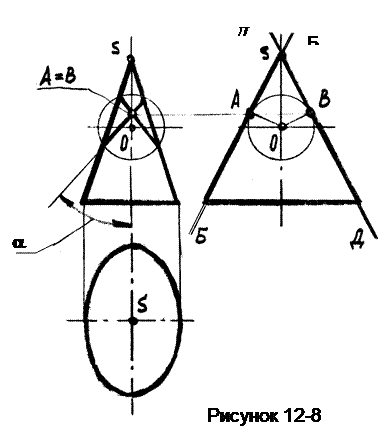 Для этого опишем сферу из некоторого центра 0, лежащего на оси конуса так, чтобы она имела двойное прикосновение с конусом и пересекала его.
Для этого опишем сферу из некоторого центра 0, лежащего на оси конуса так, чтобы она имела двойное прикосновение с конусом и пересекала его.
Точки А и В - точки двойного прикосновения, т.к. можно провести две общие касательные плоскости Б и Д.
Линия пересечения распадается на пару окружностей.
Следовательно, если пересекать поверхность эллиптического конуса плоскостью под углом a к его оси, то получим в сечении окружность.