Уравнения изопроцессов
ИЗОПРОЦЕССЫ В ИДЕАЛЬНОМ ГАЗЕ
Изопроцессами называются такие процессы, в которых какое-либо условие или параметр поддерживаются постоянными.
К характерным изопроцессам относятся следующие:
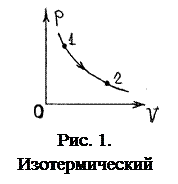1. Изотермический. Это обратимый процесс, проходящий при постоянной температуре (газ в термостате): Т=const=Т0. Для него уравнение состояния идеального газа принимает вид:
pV=νRT0=const. (1)
Это уравнение изотермы. Его график – это симметричная гипербола (рис. 1). Для любых двух точек на изотерме p1V1=p2V2.
2. Изохорный процесс. Это обратимый процесс, протекающий при постоянном объёме, т.е. в баллоне с жёсткими стенками: V=const=V0. Для него уравнение состояния pV=νRT примет вид:
.
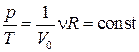Это уравнение изохоры. На изохоре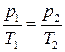 
(рис. 2).
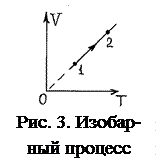
3. Изобарный процесс. Это обратимый процесс, протекающий при постоянном давлении р=р0=const. Для него уравнение состояния pV=νRT примет вид:
.
Это уравнение изобары. На изобаре 
(рис. 3).
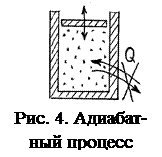4. Адиабатный процесс. Это обратимый процесс в газе, протекающий без теплообмена с окружающей средой, т.е. при котором Q=0. Адиабатный процесс может быть проведён в цилиндре с теплонепроницаемыми стенками, если поршень медленно поднимать или опускать (рис. 4). При этом энергообмен с окружающей средой происходит только в форме механической работы.
Получим уравнение адиабатного процесса аналогично трём первым. Для этого запишем первый закон термодинамики:
dQ=pdV+νCVdT.
Так как у нас dQ=0, то
νCVdT=−pdV.
Подставляя сюда р=νRT/V из уравнения состояния, получим
CVdT=−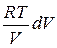
, или 
.
Интегрируя, получаем:
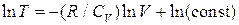, или 
=const, или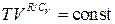 
.
А так как R=Cp−CV, то, обозначая
Ср/СV=γ,
получаем:
TVγ−1=const. (2)
Это и есть уравнение адиабаты в координатах (V,Т).
Замечание. Величина γ=Ср/СV называется показателем адиабаты.
Получим уравнение адиабаты в координатах (р,V). Для этого подставим в (2)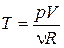 
из уравнения состояния. Это даёт: 
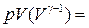const, или
pVγ=соnst. (3)
И, наконец, получим уравнение адиабаты в координатах (р,Т). Для этого подставим в (2) 
из уравнения состояния. Это даёт:
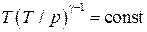, или Тγ р1−γ=const, или
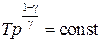. (4)
Замечание 1. Уравнение адиабаты (3) похоже на уравнение изотермы (1), только график р(V) у адиабаты идёт круче, так как γ=Ср/СV>1 (рис. 5).
Замечание 2. Так как СV=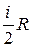
, Ср=СV+R=
, то
.
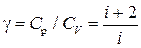Для 1-атомных газов (i=3) γ=5/3,
для 2-атомных газов (i=5) γ=7/5=1,4,
для многоатомных газов (i=6) γ=4/3.
4.2. Теплоёмкости идеального газа при изопроцессах
Вычислим молярную теплоёмкость идеального газа при различных изопроцессах в соответствии с её определением
С=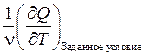
.
1. Изотермический процесс:
∞.
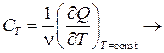Здесь всё сообщённое газу тепло Q идёт на совершение работы:
dQ=pdV+νCVdT|T=const=pdV=dA.
2. Изохорный процесс:
.
Здесь тепло идёт только на нагрев газа: dQ=νCVdT=dU.
3. Изобарный процесс:
.
Здесь тепло идёт и на нагрев, и на совершение газом работы: dQ=dU+pdV.
4. Адиабатный процесс:
.
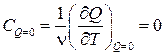