Основные определения

Случайные величины и распределения вероятностей

· Случайная величина и ее значение X

· Множество значений: конечное счетное, бесконечное счетное, бесконечное несчетное

· Соответственно величины: дискретные, непрерывные

· Область определения случайной величины: конечная, бесконечная

· Соответственно случайная величина: ограниченная, полуограниченная, неограниченная

3.2. Законы распределения дискретной случайной величины

· Ряд распределения X_i « P_i ; многоугольник распределения – графическая иллюстрация

· Условие нормировки ряда распределения:

· Функция распределения - рисунок

· Свойства функции распределения:

1.

2. 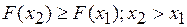- функция неубывающая

3.

4. - одна из форм условия нормировки

· Вероятность попадания в интервал

 

3.3. Законы распределения непрерывной случайной величины

· Функция распределения для непрерывной и дискретно-непрерывной случайной величины - рисунки

· Свойства функции распределения: те же, что и для дискретной случайной величины

· Вероятность попадания в интервал – так же, как и для дискретной случайной величины

· При уменьшении интервала до нуля вероятность попадания в интервал стремится к нулю

· Вероятность конкретного значения непрерывной случайной величины равна нулю, но это не означает невозможности такого события, а лишь то, что при повторении опытов это событие будет появляться сколь угодно редко. Ср.: масса точки равна нулю, но тело, составленное из точек, имеет реальную массу.

· Плотность вероятности

· И наоборот:

· Вероятность попадания в интервал (x₁, x₂)

· Элемент вероятности – вероятность попадания в интервал (x, x+dx):

· Условие нормировки:

· Плотность вероятности для дискретных и дискретно-непрерывных случайных величин вводится с помощью дельта-функций – пояснить.