Двумерные случайные величины.

Случайные векторы (системы нескольких случайных величин). Закон распределения веро-ятностей дискретной двумерной случайной величины. Функция распределения и плот-ность распределения двумерной случайной величины, их свойства. Вероятность попада-ния случайной точки в произвольную область. Отыскание плотностей вероятности со-ставляющих двумерной случайной величины. Равномерное распределение на плоскости.

Лекция 8.

Наряду с одномерными случайными величинами, возможные значения которых определяют-ся одним числом, теория вероятностей рассматривает и многомерные случайные величины. Каждое возможное значение такой величины представляет собой упорядоченный набор нескольких чисел. Геометрической иллюстрацией этого понятия служат точки п-мерного пространства, каждая координата которых является случайной величиной (дискретной или непрерывной), или п-мерные векторы. Поэтому многомерные случайные величины называют еще случайными векторами.

 

1. Дискретные двумерные случайные величины.

 

Закон распределения дискретной двумерной случайной величины (Х, Y)имеет вид таблицы с двойным входом, задающей перечень возможных значений каждой компоненты и вероятности p(x_i, y_j), с которыми величина принимает значение (x_i, y_j):

Y	Х
x1	x2	…	xi	…	xn
y1	p(x1, y1)	p(x2, y1)	…	p(xi, y1)	…	p(xn, y1)
…	…	…	…	…	…	…
yj	p(x1, yj)	p(x2, yj)	…	p(xi, yj)	…	p(xn, yj)
…	…	…	…	…	…	…
ym	p(x1, ym)	p(x2, ym)	…	p(xi, ym)	…	p(xn, ym)

 

При этом сумма вероятностей, стоящих во всех клетках таблицы, равна 1.

Зная закон распределения двумерной случайной величины, можно найти законы распреде-ления ее составляющих. Действительно, событие Х = х₁ представляется собой сумму несовместных событий (X = x₁, Y = y₁), (X = x₁, Y = y₂),…, (X = x₁, Y = y_m), поэтому

р(Х = х₁) = p(x₁, y₁) + p(x₁, y₂) +…+ p(x₁, y_m) (в правой части находится сумма вероятностей, стоящих в столбце, соответствующем Х = х₁). Так же можно найти вероятности остальных возможных значений Х. Для определения вероятностей возможных значений Y нужно сложить вероятности, стоящие в строке таблицы, соответствующей Y = y_j.

Пример 1. Дан закон распределения двумерной случайной величины:

Y	X
-2
-0,8	0,1	0,3	0,1
-0,5	0,15	0,25	0,1

 

Найти законы распределения составляющих.

Решение. Складывая стоящие в таблице вероятности «по столбцам», получим ряд распре-деления для Х:

Х	-2
р	0,25	0,55	0,2

 

Складывая те же вероятности «по строкам», найдем ряд распределения для Y:

Y	-0,8	-0,5
p	0,5	0,5

 

2. Непрерывные двумерные случайные величины.

 

Определение 8.1. Функцией распределения F(x, y)двумерной случайной величины (X, Y) называется вероятность того, что X < x, a Y < y:

F( х, у ) = p ( X < x, Y < y ). (8.1)

y

Рис.1.

Это означает, что точка (X, Y) попадет в область, заштрихованную на рис. 1, если вершина прямого угла располагается в точке (х, у).

Замечание. Определение функции распределения справедливо как для непрерывной, так и для дискретной двумерной случайной величины.

Свойства функции распределения.

1) 0 ≤ F(x, y) ≤ 1 (так как F(x, y) является вероятностью).

2) F(x, y) есть неубывающая функция по каждому аргументу:

F(x₂, y) ≥ F(x₁, y), если x₂ > x₁;

F(x, y₂) ≥ F(x, y₁), если y₂ > y₁.

Доказательство. F(x₂, y) = p(X < x₂, Y < y) = p(X < x₁, Y < y) + p(x₁ ≤ X < x₂, Y < y) ≥

≥ p(X < x₁, Y < y) = F(x₁, y). Аналогично доказывается и второе утверждение.

3) Имеют место предельные соотношения:

а) F(-∞, y) = 0; b) F(x, - ∞) = 0; c) F(- ∞, -∞) = 0; d) F( ∞, ∞) = 1.

Доказательство. События а), b) и с) невозможны ( так как невозможно событие Х<- ∞ или Y <- ∞), а событие d) достоверно, откуда следует справедливость приведенных равенств.

4) При у = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Х:

F(x, ∞) = F₁(x).

При х = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Y :

F( ∞, y) = F₂(y).

Доказательство. Так как событие Y < ∞ достоверно, то F(x, ∞) = р(Х < x) = F₁(x). Аналогично доказывается второе утверждение.

Определение 8.2. Плотностью совместного распределения вероятностей (двумер-ной плотностью вероятности)непрерывной двумерной случайной величины называ-ется смешанная частная производная 2-го порядка от функции распределения:

. (8.2)

Замечание. Двумерная плотность вероятности представляет собой предел отношения вероятности попадания случайной точки в прямоугольник со сторонами Δх и Δу к площади этого прямоугольника при

Свойства двумерной плотности вероятности.

1) f(x, y) ≥ 0 (см. предыдущее замечание: вероятность попадания точки в прямоуголь-ник неотрицательна, площадь этого прямоугольника положительна, следовательно, предел их отношения неотрицателен).

2) (cледует из определения двумерной плотности вероятно-сти).

3) (поскольку это вероятность того, что точка попадет на плос-кость Оху, то есть достоверного события).

Вероятность попадания случайной точки в произвольную область.

Пусть в плоскости Оху задана произвольная область D. Найдем вероятность того, что точка, координаты которой представляют собой систему двух случайных величин (двумерную случайную величину) с плотностью распределения f(x, y), попадет в область D. Разобьем эту область прямыми, параллельными осям координат, на прямоугольники со сторонами Δх и Δу. Вероятность попадания в каждый такой прямоугольник равна 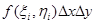, где - координаты точки, принадлежащей прямоугольнику. Тогда вероятность попадания точки в область D есть предел интегральной суммы 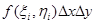, то есть

(8.3)

Отыскание плотностей вероятности составляющих

двумерной случайной величины.

Выше было сказано, как найти функцию распределения каждой составляющей, зная двумерную функцию распределения. Тогда по определению плотности распределения

(8.4)

Аналогично находится (8.4′)