Корректируем план.

Преобразуем матрицу стоимости

0 9 0 11 0
0 13 -1 0 -2
5 12 0 15 0
1 0 -11 8 0
2 30 16 25 0

Т.к. матрица содержит отрицательные элементы, то план не является оптимальным.

7. Выбираем максимальный по модулю отрицательный элемент матрицы (-11).

8. Из клетки этого элемента строим цикл по другим выделенным элементам, вершины нумеруем.

0 9 0 11 0
0 13 -1 0 -2
5 12 II 0 15 III 0
1 0 I -11 8 IV 0
2 30 16 25 0

 

9. Найденный цикл переносим на транспортную таблицу. Из четных вершин цикла, выбираем вершину с минимальным объемом перевозок: 185; 30.
Таким образом min=30.

145 13 9 13 6 15 14
155 20 20 19 245 2 19
10 4 II 5 185 2 III 6 85
19 20 5 I 7 8 IV 19 30
3 18 17 8 40 2

 

10. Из четных вершин этот объем вычитается, а в нечетных прибавляется.
Получаем новый план.

145 13 9 13 6 15 14
155 20 20 19 245 2 19
10 4 155 5 2 115 2
19 20 5 30 7 8 19
3 18 17 8 402

11. Определяем новые затраты.

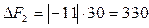, (ден.ед).

12. Проверяем новый план на оптимальность, выполняя вновь пункты с 5 по 11.

-13 -11 -13 -14 vi ui
13 9 13 6 14
20 20 19 2 19 -7
10 4 5 2 6
19 5 7 8 19
3 18 17 8 2
0 I -2 0 11 II 0
0 2 -1 0 -2
5 1 IV 0 15 III 0
12 VI 0 V 0 19 11
2 19 16 25 0

 

 

 

Найденный цикл переносим на транспортную таблицу. Из четных вершин цикла, выбираем вершину с минимальным объемом перевозок: 15; 155, 20.
Таким образом min=15.

145 13 I 9 13 6 II1514
155 20 20 19 245 2 19
10 4 IV 5 155 2 III 6 115
19 VI 5 20 V 7 30 8 19
3 18 17 8 40 2
145 13 15 9 13 6 14
155 20 20 19 245 2 19
10 4 140 5 2 130 2
19 5 5 45 7 8 19
3 18 17 8 40 2

Определяем новые затраты.

, (ден. ед.)

-13 -9 -11 -12 vi ui
13 9 13 6 14
20 20 19 2 19 -7
10 4 5 2 6
19 5 7 8 19
3 18 17 8 2
0 0 2 11 2
0 4 1 0 0
3 1 0 13 0
10 0 0 17 11
0 19 16 23 0

 

Т.к. преобразованная матрица в базисных клетках содержит нули, а элементы в остальных клетках неотрицательные, то полученный план является оптимальным.

Таким образом, необходимо осуществить 9 перевозок по следующим маршрутам:

Суммарные затраты при перевозках составят: F=7510 (ден. ед.).